题目内容
在平面直角坐标系xoy中,设抛物线C:y2=4x
(1)求抛物线C上到焦点距离等于5的点的横坐标;
(2)设命题p:过抛物线C上一点M(1,2)作两条不同的直线,分别交抛物线C于点A,B,设直线MA,MB,AB的斜率均存在且分别记为kMA,kMB,kAB若
+
为定值,则kAB为定值.判断命题p的真假,并证明;
(3)写出(2)中命题p的逆命题,并判断真假(不要求证明).
(1)求抛物线C上到焦点距离等于5的点的横坐标;
(2)设命题p:过抛物线C上一点M(1,2)作两条不同的直线,分别交抛物线C于点A,B,设直线MA,MB,AB的斜率均存在且分别记为kMA,kMB,kAB若
| 1 |
| kMA |
| 1 |
| kMB |
(3)写出(2)中命题p的逆命题,并判断真假(不要求证明).
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设抛物线C上一点的横坐标为x,由题意,根据抛物线定义,得x+1=5,由此能求出抛物线C上到焦点距离等于5的点的横坐标.
(2)设A(x1,y1),B(x2,y2),且x1≠x2,y1≠y2,则
+
=
+
,kAB=
,由此能证明当
+
为定值时,kAB为定值.
(3)把命题p的题设和结论互换,能求出逆命题,命题p的逆命题是真命题.
(2)设A(x1,y1),B(x2,y2),且x1≠x2,y1≠y2,则
| 1 |
| kMA |
| 1 |
| kMB |
| x1-1 |
| y1-2 |
| x2-1 |
| y2-2 |
| y1-y2 |
| x1-x2 |
| 1 |
| kMA |
| 1 |
| kMB |
(3)把命题p的题设和结论互换,能求出逆命题,命题p的逆命题是真命题.
解答:
解:(1)设抛物线C上一点的横坐标为x,
由题意,根据抛物线定义,得x+1=5,解得x=4,
∴抛物线C上到焦点距离等于5的点的横坐标为4.
(2)设A(x1,y1),B(x2,y2),且x1≠x2,y1≠y2,
则
+
=
+
,kAB=
,
∵点A,B在抛物线C上,
∴
,即
,
代入上式,化简得:
+
=
+
=
+
=
+1,
kAB=
=
,
∴
+
为定值时,y1+y2为定值,∴kAB为定值.
(3)命题p的逆命题:
过抛物线C上一点M(1,2)作两条不同的直线,分别交抛物线C于A,B,设直线MA,MB,AB的斜率均存在且分别记为kMA,kMB,kAB,若kAB为定值,则
+
为定值.
命题p的逆命题是真命题.
由题意,根据抛物线定义,得x+1=5,解得x=4,
∴抛物线C上到焦点距离等于5的点的横坐标为4.
(2)设A(x1,y1),B(x2,y2),且x1≠x2,y1≠y2,
则
| 1 |
| kMA |
| 1 |
| kMB |
| x1-1 |
| y1-2 |
| x2-1 |
| y2-2 |
| y1-y2 |
| x1-x2 |
∵点A,B在抛物线C上,
∴
|
|
代入上式,化简得:
| 1 |
| kMA |
| 1 |
| kMB |
| y12-4 |
| 4(y1-2) |
| y22-4 |
| 4(y2-2) |
| y1+2 |
| 4 |
| y2+2 |
| 4 |
| y1+y2 |
| 4 |
kAB=
| 4(y1-y2) |
| y12-y22 |
| 4 |
| y1+y2 |
∴
| 1 |
| kMA |
| 1 |
| kMB |
(3)命题p的逆命题:
过抛物线C上一点M(1,2)作两条不同的直线,分别交抛物线C于A,B,设直线MA,MB,AB的斜率均存在且分别记为kMA,kMB,kAB,若kAB为定值,则
| 1 |
| kMA |
| 1 |
| kMB |
命题p的逆命题是真命题.
点评:本题考查抛物线上点的横坐标的求法,考查直线的斜率为定值的证明,考查命题的逆命题的求法,解题时要注意函数与方程思想的合理运用.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
关于x的不等式sin2x+acosx-a2≤1+cosx对一切x∈R恒成立,则实数a的取值范围为( )
A、(-1,
| ||
B、[-1,
| ||
C、(-∞,-1]∪[
| ||
D、(-∞,-1)∪(
|
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E是棱BC上的一点,则三棱锥D1-B1C1E的体积等于( )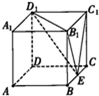

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=2x-
的零点在区间( )
| 1 |
| x |
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
函数y=sin(2x-
)在区间[
,
]上的值域是( )
| π |
| 6 |
| π |
| 12 |
| π |
| 2 |
A、[-
| ||
B、[
| ||
| C、[0,1] | ||
D、[0,
|
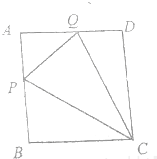 如图,正方形ABCD的边长为1,点P,Q分别在边AB,AD上,且PQ=1,设AP+AQ=x,记△CPQ的面积函数为S=f(x).
如图,正方形ABCD的边长为1,点P,Q分别在边AB,AD上,且PQ=1,设AP+AQ=x,记△CPQ的面积函数为S=f(x).