题目内容
5.在△ABC中,内角A,B,C对应的边长分别为a,b,c,已知$\overrightarrow{m}$=(c,a+b),$\overrightarrow{n}$=(a-b,acosB-$\frac{1}{2}$b),$\overrightarrow{m}$∥$\overrightarrow{n}$.(I)求角A;
(II)若a=$\sqrt{3}$,求b+c的取值范围.
分析 (I)根据平面向量的共线定理,利用余弦定理即可求出A的值;
(II)由正弦定理求出b、c的表达式,计算b+c的取值范围即可.
解答 解:(I)∵$\overrightarrow{m}$∥$\overrightarrow{n}$,∴c•(acosB-$\frac{1}{2}$b)-(a+b)(a-b)=0,
即c(acosB-$\frac{1}{2}$b)=a2-b2,-----(1分)
由余弦定理得
a2+c2-b2-bc=2a2-2b2,a2=b2+c2-bc;------(3分)
∵a2=b2+c2-2bccosA,∴cosA=$\frac{1}{2}$;--------(4分)
∵A∈(0,π),∴A=$\frac{π}{3}$;--------(5分)
(II)由正弦定理得$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2,
∴b=2sinB,c=2sinC-----(6分)
∴b+c=2sinB+2sinC=2sinB+2sin(A+B)-------(7分)
=2sinB+2sinAcosB+2cosAsinB
=2sinB+2×$\frac{\sqrt{3}}{2}$cosB+2×$\frac{1}{2}$sinB
=3sinB+$\sqrt{3}$cosB
=2$\sqrt{3}$sin(B+$\frac{π}{6}$);--------(9分)
∵B∈(0,$\frac{2π}{3}$),∴B+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{5π}{6}$),
∴sin(B+$\frac{π}{6}$)∈($\frac{1}{2}$,1];--------(11分)
所以b+c∈($\sqrt{3}$,2$\sqrt{3}$].--------(12分)
点评 本题考查了平面向量的共线定理以及正弦、余弦定理的应用问题,是综合性题目.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案| A. | 2或$\frac{5}{2}$ | B. | ±2 | C. | 2 | D. | -2 |
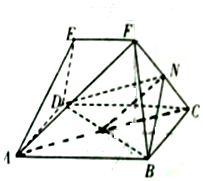 如图,在多面体ABCDEF中,四边形ABCD为矩形,△ADE,△BCF均为等边三角形,EF∥AB,EF=AD=$\frac{1}{2}$AB,N为线段PC的中点.
如图,在多面体ABCDEF中,四边形ABCD为矩形,△ADE,△BCF均为等边三角形,EF∥AB,EF=AD=$\frac{1}{2}$AB,N为线段PC的中点.