题目内容
8.某高校《统计初步》课程的教师随机调查了选修该课的学生的一些情况,具体数据如表1:为了判断主修统计专业是否与性别有关,根据表中数据,得K2的观察值为k=$\frac{{50×{{(13×20-10×7)}^2}}}{23×27×20×30}$≈4.844,所以判断主修统计专业与性别有关,那么这种判断出错的可能性不超过( )| 表1 | 非统计专业 | 统计专业 |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
| P(K2≥k0) | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
| A. | 5% | B. | 2.5% | C. | 1% | D. | 0.5% |
分析 由题意知根据表中所给的数据得到观测值是4.844,从临界值表中可以知道4.844>3.841,根据临界值表中所给的概率得到与本题所得的数据对应的概率是0.05,得到结论.
解答 解:∵由题意知为了判断主修统计专业是否与性别有关系,
根据表中的数据,得到K2≈4.844,
∵K2≥3.841,
由临界值表可以得到P(K2≥3.841)=0.05
∴判定主修统计专业与性别有关系的这种判断出错的可能性为0.05=5%.
故选:A.
点评 独立性检验是考查两个分类变量是否有关系,并且能较精确的给出这种判断的可靠程度的一种重要的统计方法,主要是通过k2的观测值与临界值的比较解决的.

练习册系列答案
相关题目
16.已知集合U={-5,-3,1,2,3,4,5,6},集合A={x|x2-7x+12=0},集合B={a2,2a-1,6}.若A∩B={4},且B⊆U,则a等于( )
| A. | 2或$\frac{5}{2}$ | B. | ±2 | C. | 2 | D. | -2 |
3.若事件A与B互斥,已知P(A)=P(B)=$\frac{1}{4}$,则P(A∪B)的值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{16}$ | D. | 0 |
18.已知不等式组$\left\{\begin{array}{l}{2x+y-3≤0}\\{x-y+2≥0}\\{2x-3y-3≤0}\end{array}\right.$表示的平面区域为D,P(x,y)为D上一点,则|x+4|+|y+3|的最大值为( )
| A. | $\frac{17}{2}$ | B. | 9 | C. | $\frac{29}{3}$ | D. | 10 |
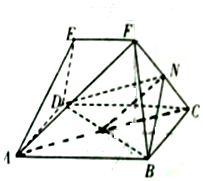 如图,在多面体ABCDEF中,四边形ABCD为矩形,△ADE,△BCF均为等边三角形,EF∥AB,EF=AD=$\frac{1}{2}$AB,N为线段PC的中点.
如图,在多面体ABCDEF中,四边形ABCD为矩形,△ADE,△BCF均为等边三角形,EF∥AB,EF=AD=$\frac{1}{2}$AB,N为线段PC的中点.