题目内容
12．若点P（a，b）在函数y=-x2+3lnx的图象上，点Q（c，d）在函数y=x+2的图象上，则|PQ|的最小值为2$\sqrt{2}$．分析 先求出与直线y=x+2平行且与曲线y=-x2+3lnx相切的直线y=x+m．再求出此两条平行线之间的距离，即可得出结论．
解答 解：设直线y=x+m与曲线y=-x2+3lnx相切于P（x0，y0），
由函数y=-x2+3lnx，∴y′=-2x+$\frac{3}{x}$，
令-2x0+$\frac{3}{{x}_{0}}$=1，又x0＞0，解得x0=1．
∴y0=-1+3ln1=-1，
可得切点P（1，-1）．
代入-1=1+m，解得m=-2．
可得与直线y=x+2平行且与曲线y=-x2+3lnx相切的直线y=x-2．
而两条平行线y=x+2与y=x-2的距离d=2$\sqrt{2}$．
故答案为2$\sqrt{2}$．
点评 本题考查了导数的几何意义、切线的方程、两条平行线之间的距离、最小值的转化问题等基础知识与基本技能方法，属于中档题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
2．
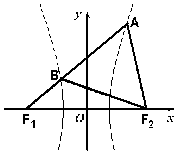如图，F1、F2分别是双曲线的左、右焦点，过F1的直线与双曲线的左、右两支分别相交于B、A两点，若△ABF2为等边三角形，则该双曲线的离心率为（ ）
如图，F1、F2分别是双曲线的左、右焦点，过F1的直线与双曲线的左、右两支分别相交于B、A两点，若△ABF2为等边三角形，则该双曲线的离心率为（ ）| A． | $\sqrt{3}$ | B． | $\sqrt{5}$ | C． | $\sqrt{7}$ | D． | 3 |
3．若函数f（2x+1）的定义域为（-1，0），则函数f（x）的定义域为（ ）
| A． | （-2，0） | B． | （-1，0） | C． | （-1，1） | D． | （0，1） |
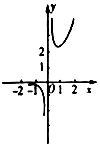
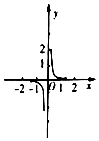
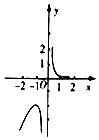
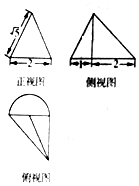某几何体上的三视图如图所示，则该几何体的体积是$\frac{4+π}{3}$．