题目内容
7.某人打算制定一个长期储蓄计划,每年年初存款2万元,连续储蓄12年.由于资金原因,从第7年年初开始,变更为每年年初存款1万元.若存款利率为每年2%,且上一年年末的本息和共同作为下一年年初的本金,则第13年年初的本息和约为20.9万元(结果精确到0.1).(参考数据:1.026≈1.13,1.0212≈1.27)分析 确定每年的本息和,利用等比数列的求和公式,即可得到结论.
解答 解:由题意,第13年年初的本息和为2(1.0212+1.0211+…+1.027)+(1.026+1.025+…+1.02)
=2×$\frac{1.0{2}^{7}(1-1.0{2}^{6})}{1-1.02}$+$\frac{1.02×(1-1.0{2}^{6})}{1-1.02}$≈20.9.
故答案为20.9.
点评 本题考查学生的阅读分析能力,数列模型的建立能力,属于基础题目.

练习册系列答案
相关题目
17.在长方体ABCD-A1B1C1D1中,底面ABCD的边长为a的正方形,E是CC1的中点,若该长方体的外接球的表面积为10πa2,则异面直线AE与C1D1所成的角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
18.表面积为3π的圆锥的侧面展开图是一个半圆,则该圆锥的底面圆半径为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.若实数x,y满足$\left\{\begin{array}{l}x+y≤2\\ 2x+y≥0\\ 3x-y-2≤0\end{array}\right.$,则$\frac{y}{1-x}$的取值范围为( )
| A. | $({-∞,-\frac{4}{3}}]$ | B. | $({-∞,\frac{3}{4}})$ | C. | $[{-\frac{3}{4},+∞})$ | D. | $[{-\frac{4}{3},+∞})$ |
19.已知实数x,y满足约束条件$\left\{\begin{array}{l}{|x-2y+2|≤2}\\{|x+3y-8|≤2}\end{array}\right.$,则z=x+2y的最大值为( )
| A. | 4 | B. | 8 | C. | $\frac{24}{5}$ | D. | $\frac{36}{5}$ |
17.已知数列{an}的通项公式为an=$\frac{1}{n(n+2)}$,前n项和为Sn,若实数λ满足(-1)nλ<3+(-1)n+1Sn对任意正整数n恒成立,则实数λ的取值范围是( )
| A. | $-\frac{10}{3}$<λ≤$\frac{9}{4}$ | B. | $-\frac{10}{3}$<λ<$\frac{9}{4}$ | C. | $-\frac{9}{4}$<λ≤$\frac{10}{3}$ | D. | $-\frac{9}{4}$<λ<$\frac{10}{3}$ |
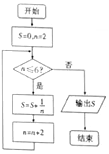 如图所示的程序框图中,输出的S的值为$\frac{11}{12}$.
如图所示的程序框图中,输出的S的值为$\frac{11}{12}$.