题目内容
17.函数f(x)=$\frac{{e}^{x}}{x}$的图象可能是下列图形中的( )| A. |  | B. | 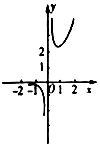 | C. | 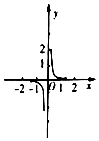 | D. | 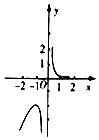 |
分析 利用x的范围,判断函数的值的范围,然后利用函数的导数,判断函数的单调性即可.
解答 解:函数f(x)=$\frac{{e}^{x}}{x}$,可知x<0,y<0;
当x>0时,函数f′(x)=$\frac{{xe}^{x}-{e}^{x}}{{x}^{2}}$,令f′(x)=0,可得x=1.
当x∈(0,1),f′(x)<0,函数f(x)=$\frac{{e}^{x}}{x}$是减函数,
x>1时,f′(x)>0,函数f(x)=$\frac{{e}^{x}}{x}$是增函数,
函数图象B,A满足,C,D不正确;
当x<0时,函数f′(x)=$\frac{{xe}^{x}-{e}^{x}}{{x}^{2}}$<0,函数是减函数,所以B正确,A不正确.
故选:B.
点评 本题考查函数的图象的判断,利用导数判断函数的单调性,考查转化思想以及分类讨论思想的应用.

练习册系列答案
相关题目
8.命题“所有能被7整除的数都是奇数”的否定是( )
| A. | 所有不能被7整除的数都是奇数 | B. | 所有能被7整除的数都不是奇数 | ||
| C. | 存在一个不能被7整除的数是奇数 | D. | 存在一个能被7整除的数不是奇数 |
2.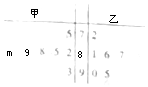 甲、乙两同学在本学期的7次考试中获得的成绩如茎叶图所示,两人各有一次成绩看不清楚,其中m,n∈Z,已知两位同学各自的7次成绩各不相同,但两人7次成绩的平均分相同,则两人7次成绩的中位数恰好也相同的概率为( )
甲、乙两同学在本学期的7次考试中获得的成绩如茎叶图所示,两人各有一次成绩看不清楚,其中m,n∈Z,已知两位同学各自的7次成绩各不相同,但两人7次成绩的平均分相同,则两人7次成绩的中位数恰好也相同的概率为( )
 甲、乙两同学在本学期的7次考试中获得的成绩如茎叶图所示,两人各有一次成绩看不清楚,其中m,n∈Z,已知两位同学各自的7次成绩各不相同,但两人7次成绩的平均分相同,则两人7次成绩的中位数恰好也相同的概率为( )
甲、乙两同学在本学期的7次考试中获得的成绩如茎叶图所示,两人各有一次成绩看不清楚,其中m,n∈Z,已知两位同学各自的7次成绩各不相同,但两人7次成绩的平均分相同,则两人7次成绩的中位数恰好也相同的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
 某同学收集了班里9名男生50m跑的测试成绩(单位:s):
某同学收集了班里9名男生50m跑的测试成绩(单位:s):