题目内容
1.已知抛物线${C_1}:{y^2}=8x$的焦点为F,P是抛物线C1上位于第一象限内的点,|PF|=4,P到双曲线${C_2}:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0\;\;,\;\;b>0})$的一条渐近线的距离为2,则双曲线C2的离心率为$\frac{5}{4}$.分析 利用抛物线的性质求出P的坐标,写出双曲线的局限性方程,推出a,b关系然后求解双曲线的离心率.
解答 解:抛物线${C_1}:{y^2}=8x$的焦点为F(2,0),P是抛物线C1上位于第一象限内的点,|PF|=4,P(2,4),
P(2,4)到双曲线${C_2}:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0\;\;,\;\;b>0})$的一条渐近线bx-ay=0的距离为2,
可得:$\frac{|2b-4a|}{\sqrt{{a}^{2}+{b}^{2}}}$=2,可得:4b=3a,
即:16c2-16a2=9a2,
∴$\frac{c}{a}$=$\frac{5}{4}$.
故答案为:$\frac{5}{4}$.
点评 本题考查抛物线以及双曲线的简单性质的应用,考查计算能力.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
11.已知点M的坐标(x,y)满足不等式组$\left\{\begin{array}{l}{2x+y-4≥0}\\{x-y-2≤0}\\{y-3≤0}\end{array}\right.$,N为直线y=-2x+2上任一点,则|MN|的最小值是( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | 1 | D. | $\frac{\sqrt{17}}{2}$ |
13.已知△ABC的三边长a,b,c成递减的等差数列,若$B=\frac{π}{4}$,则cosA-cosC=( )
| A. | $-\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $-\root{4}{2}$ | D. | $\root{4}{2}$ |
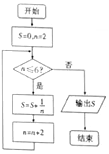 如图所示的程序框图中,输出的S的值为$\frac{11}{12}$.
如图所示的程序框图中,输出的S的值为$\frac{11}{12}$. 已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.