题目内容
已知等差数列{an}满足a3=8，a6=17．
（1）求{an}的通项公式；
（2）各项均为正数的等比数列{bn}满足b1=a1，b3=a3，求数列{bn}的通项公式．
（1）求{an}的通项公式；
（2）各项均为正数的等比数列{bn}满足b1=a1，b3=a3，求数列{bn}的通项公式．
考点：等比数列的通项公式,等差数列的通项公式
专题：等差数列与等比数列
分析：（1）由已知条件利用等差数列通项公式，列出方程组，求出首项和公差，由此能求出{an}的通项公式．
（2）由已知条件利用等比数列通项公式，列出方程组，求出首项和公比，由此能求出数列{bn}的通项公式．
（2）由已知条件利用等比数列通项公式，列出方程组，求出首项和公比，由此能求出数列{bn}的通项公式．
解答：
（本题满分（13分），第（1）问（6分），第（2）问7分）
解：（1）设等差数列{an}的首项为a1，公差为d，
依题意有：
，
解得：
，
∴an=3n-1．（6分）
（2）依题意设bn=b1qn-1，
∵等比数列{bn}满足b1=a1，b3=a3，
∴
，
∵{bn}为正项等比数列，∴q＞0，
解得
，∴bn=2n．…（13分）
解：（1）设等差数列{an}的首项为a1，公差为d，
依题意有：
|
解得：
|
∴an=3n-1．（6分）
（2）依题意设bn=b1qn-1，
∵等比数列{bn}满足b1=a1，b3=a3，
∴
|
∵{bn}为正项等比数列，∴q＞0，
解得
|
点评：本题考查数列的通项公式的求法，解题时要认真审题，注意等差数列和等比数列的性质的灵活运用．
练习册系列答案
相关题目
已知等腰Rt△ABC，BC⊥AC，将△ABC绕着边AB旋转θ角到△ABC′，连接CC′，D为线段CC′的中点，P是线段AB上任一点．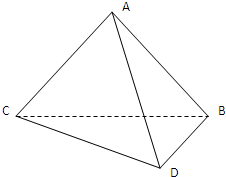
如图，平面ABC⊥平面DBC，已知AB=AC，BC=6，∠BAC=∠DBC=90°，∠BDC=60° 
已知F为抛物线E：y2=2px（P＞0）的焦点，抛物线上点G的横坐标为2，且满足|GF|=3．