题目内容
已知函数f(x)=(
m2-m)x2+m+1.
(1)若函数y=lgf(x)的定义域为R,求实数m的取值范围;
(2)设命题p:?x∈[
,2],f(x)≥3.若命题p为假命题,求实数m的取值范围.
| 1 |
| 2 |
(1)若函数y=lgf(x)的定义域为R,求实数m的取值范围;
(2)设命题p:?x∈[
| 1 |
| 2 |
考点:二次函数的性质,函数的值域
专题:函数的性质及应用
分析:(1)由题意可得(
m2-m)x2+m+1>0的解集为R.若
m2-m=0,即m=0或m=2,均符合题意;若
m2-m≠0,则
解不等式,综合可得;(2)问题等价于(
m2-m)x2+m-2≥0在x∈[
,2]上恒成立.设h(x)=(
m2-m)x2+m-2,分
m2-m=0,
m2-m>0,
m2-m<0,可得m的范围,取其补集即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)由函数y=lgf(x)的定义域为R可知(
m2-m)x2+m+1>0的解集为R.
若
m2-m=0,即m=0或m=2,均符合题意;
若
m2-m≠0,则
,解得-1<m<0或m>2.
综上,实数m的取值范围是(-1,0]∪[2,+∞);
(2)若命题p为真命题,则(
m2-m)x2+m-2≥0在x∈[
,2]上恒成立.
设h(x)=(
m2-m)x2+m-2,
若
m2-m=0,即m=0或m=2,代入知m=2符合;
若
m2-m>0,则h(
)≥0,即
×(
m2-m)+m-2≥0,解得m≤-8或m>2;
若
m2-m<0,则h(2)≥0,即4(
m2-m)+m-2≥0,无解.
综上,若命题p为真命题,实数m的取值范围是m≤-8或m≥2,
∴当命题p为假命题时,实数m的取值范围是(-8,2).
| 1 |
| 2 |
若
| 1 |
| 2 |
若
| 1 |
| 2 |
|
综上,实数m的取值范围是(-1,0]∪[2,+∞);
(2)若命题p为真命题,则(
| 1 |
| 2 |
| 1 |
| 2 |
设h(x)=(
| 1 |
| 2 |
若
| 1 |
| 2 |
若
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
若
| 1 |
| 2 |
| 1 |
| 2 |
综上,若命题p为真命题,实数m的取值范围是m≤-8或m≥2,
∴当命题p为假命题时,实数m的取值范围是(-8,2).
点评:本题考查二次函数的性质,涉及分类讨论和函数的值域,属基础题.

练习册系列答案
相关题目
设离散型随机变量ξ的概率分布如下:则表中的a的值为( )
| ξ | 1 | 2 | 3 | 4 | ||||||
| P |
|
|
| a |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
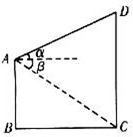 如图,两座建筑物AB,CD的底部都在同一个水平面上,且AB、CD均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看点D的仰角为α,看点C的俯角为β,已知α+β=45°,则BC的长度是
如图,两座建筑物AB,CD的底部都在同一个水平面上,且AB、CD均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看点D的仰角为α,看点C的俯角为β,已知α+β=45°,则BC的长度是