题目内容
一个口袋装有5只同样大小的球,编号分别为1,2,3,4,5,从中同时取出3只,以ξ表示取出球最小的号码,求ξ的分布列.
考点:离散型随机变量及其分布列
专题:概率与统计
分析:因为同时取出3个球,ξ表示取出球的最小号码,所以ξ的取值为1,2,3.分别求出相应的概率,由此能求出ξ的分布列.
解答:
解:因为同时取出3个球,ξ表示取出球的最小号码,所以ξ的取值为1,2,3.
当ξ=1时,其他两球可在余下的4个球中任意选取,
因此P(ξ=1)=
=
,
当ξ=2时,其他两球的编号在3、4、5中选取,
因此P(ξ=2)=
=
,
当ξ=3时,其只可能为3,4,5一种情况,
其P(ξ=3)=
.
所以ξ的分布列为:
当ξ=1时,其他两球可在余下的4个球中任意选取,
因此P(ξ=1)=
| ||
|
| 3 |
| 5 |
当ξ=2时,其他两球的编号在3、4、5中选取,
因此P(ξ=2)=
| ||
|
| 3 |
| 10 |
当ξ=3时,其只可能为3,4,5一种情况,
其P(ξ=3)=
| 1 |
| 10 |
所以ξ的分布列为:
| ξ | 1 | 2 | 3 | ||||||
| P |
|
|
|
点评:本题考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题.

练习册系列答案
相关题目
一个正方体,它的表面涂满了红色.在它的每个面上切两刀可得27个小立方块,从中任取两个,其中恰有1个一面涂有红色,1个两面涂有红色的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)在R上是减函数,则有( )
| A、f(3)<f(5) |
| B、f(3)≤f(5) |
| C、f(3)>f(5) |
| D、f(3)≥f(5) |
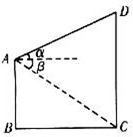 如图,两座建筑物AB,CD的底部都在同一个水平面上,且AB、CD均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看点D的仰角为α,看点C的俯角为β,已知α+β=45°,则BC的长度是
如图,两座建筑物AB,CD的底部都在同一个水平面上,且AB、CD均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看点D的仰角为α,看点C的俯角为β,已知α+β=45°,则BC的长度是