题目内容
在北纬45°的纬度圈上有A，B两地，A在东经13°，B在东经73°，设地球半径为R，则A，B两地的球面距离是 ．
考点：球面距离及相关计算
专题：计算题,空间位置关系与距离
分析：A，B两地在同一纬度圈上，计算经度差，求出AB弦长，以及球心角，然后求出球面距离．
解答：
解：由题意，AB的纬圆半径是
R，经度差是60°，所以AB=
R
设球心角是α，则cosα=
=
，
∴α=arccos
，
∴AB两地的球面距离是Rarccos
．
故答案为：Rarccos
．
| ||
| 2 |
| ||
| 2 |
设球心角是α，则cosα=
R2+R2-
| ||
| 2R2 |
| 3 |
| 4 |
∴α=arccos
| 3 |
| 4 |
∴AB两地的球面距离是Rarccos
| 3 |
| 4 |
故答案为：Rarccos
| 3 |
| 4 |
点评：本题考查球面距离及其它计算，考查空间想象能力，是基础题．其中计算出AB弧对应的球心角是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
一个正方体，它的表面涂满了红色．在它的每个面上切两刀可得27个小立方块，从中任取两个，其中恰有1个一面涂有红色，1个两面涂有红色的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）=x2-2ax+1对任意x∈（0，1]恒有f（x）≥0成立，则实数a的取值范围是（ ）
| A、[1，+∞） | ||
B、[-
| ||
| C、（-∞，1] | ||
D、（-∞，-
|
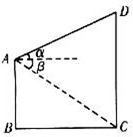如图，两座建筑物AB，CD的底部都在同一个水平面上，且AB、CD均与水平面垂直，它们的高度分别是9m和15m，从建筑物AB的顶部A看点D的仰角为α，看点C的俯角为β，已知α+β=45°，则BC的长度是