题目内容
某班5名学生的数学和物理成绩如表:
(1)画出散点图;
(2)求物理成绩y对数学成绩x的线性回归方程;
(3)一名学生的数学成绩是96分,试预测他的物理成绩.
| 学生 学科 | A | B | C | D | E |
| 数学成绩(x) | 88 | 76 | 73 | 66 | 63 |
| 物理成绩(y) | 78 | 65 | 71 | 64 | 61 |
(2)求物理成绩y对数学成绩x的线性回归方程;
(3)一名学生的数学成绩是96分,试预测他的物理成绩.
考点:线性回归方程,频率分布表
专题:应用题,概率与统计
分析:(1)根据所给数据,可得散点图;
(2)根据所给的数据利用最小二乘法.写出线性回归方程的系数和a的值,写出线性回归方程,注意运算过程中不要出错.
(2)将x=96代入所求出的线性回归方程中,得y=82,即这个学生的预测他的物理成绩为82分.
(2)根据所给的数据利用最小二乘法.写出线性回归方程的系数和a的值,写出线性回归方程,注意运算过程中不要出错.
(2)将x=96代入所求出的线性回归方程中,得y=82,即这个学生的预测他的物理成绩为82分.
解答:
解:(1)散点图如下图所示:
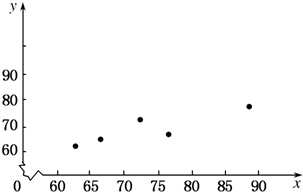
(2)
=
×(88+76+73+66+63)=73.2.
=
×(78+65+71+64+61)=67.8.
xiyi=88×78+76×65+73×71+66×64+63×61=25054.
xi2=882+762+732+662+632=27174.
∴b≈0.625.
∴a=67.8-0.625×73.2=22.05.
∴y对x的线性回归方程是y=0.625x+22.05.
(3)当x=96,则y=0.625×96+22.05≈82.
所以预测他的物理成绩是82分.

(2)
. |
| x |
| 1 |
| 5 |
. |
| y |
| 1 |
| 5 |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
∴b≈0.625.
∴a=67.8-0.625×73.2=22.05.
∴y对x的线性回归方程是y=0.625x+22.05.
(3)当x=96,则y=0.625×96+22.05≈82.
所以预测他的物理成绩是82分.
点评:本题考查线性回归方程,是一个基础题,解题的关键是利用最小二乘法写出线性回归系数,注意解题的运算过程不要出错.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
已知α∈(0,π),且sinα+cosα=
,则sinα-cosα的值为( )
| ||
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
已知动点P的竖坐标恒为2,则动点P的轨迹是( )
| A、平面 | B、直线 |
| C、不是平面也不是直线 | D、以上都不对 |
定义在R上的函数f(x)满足f(x+4)-f(x)=0,且已知x∈(0,4]时,f(x)=
,则函数g(x)=5f(x)-x零点个数为( )
|
| A、3 | B、4 | C、5 | D、6 |
函数y=3sin(2x-
)的最小正周期是( )
| π |
| 6 |
A、
| ||
B、
| ||
| C、π | ||
| D、2π |