题目内容
已知f(x)为三次函数,当x=1时f(x)有极大值4,当x=3时,f(x)有极小值0,且函数f(x)过原点,则此函数是( )
| A、f(x)=x3-2x2+3x |
| B、f(x)=x3-6x2+x |
| C、f(x)=x3+6x2+9x |
| D、f(x)=x3-6x2+9x |
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:设三次函数为y=ax3+bx2+cx+d,利用过原点,推出常数项为d=0,y'=3ax2+2bx+c,根据该函数当x=1时有极大值4,当x=3时,有极小值0,得到方程组,从而可求a,b,c,故可得三次函数.
解答:
解:设三次函数为y=ax3+bx2+cx+d
因为过原点,所以常数项为d=0
∴y=ax3+bx2+cx
∴y'=3ax2+2bx+c
由于该函数当x=1时有极大值4,当x=3时,有极小值0,
所以3ax2+2bx+c=0有两个实根1和3
∴
,
∴a=1,b=-6,c=9
所以三次函数为y=x3-6x2+9x
故选D.
因为过原点,所以常数项为d=0
∴y=ax3+bx2+cx
∴y'=3ax2+2bx+c
由于该函数当x=1时有极大值4,当x=3时,有极小值0,
所以3ax2+2bx+c=0有两个实根1和3
∴
|
∴a=1,b=-6,c=9
所以三次函数为y=x3-6x2+9x
故选D.
点评:本题以函数的性质为载体,考查函数解析式的求解,解题的关键是正确运用导数,合理建立方程组.

练习册系列答案
相关题目
已知集合A{x|y=lg(2-x)},集合B={x|-2≤x≤2},则A∩B=( )
| A、{x|x≥-2} |
| B、{x|-2<x<2} |
| C、{x|-2≤x<2} |
| D、{x|x<2} |
三棱柱ABC-A1B1C1中,AA1=2且AA1⊥平面ABC,△ABC是边长为
的正三角形,该三棱柱的六个顶点都在一个球面上,则这个球的体积为( )
| 3 |
| A、8π | ||||
B、
| ||||
C、
| ||||
D、8
|
双曲线
-
=1的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r等于( )
| x2 |
| 12 |
| y2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线C:
-
=1的焦距为10,点P(1,2)在C的渐近线上,则C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知某空间几何体的三视图如图所示,则( )
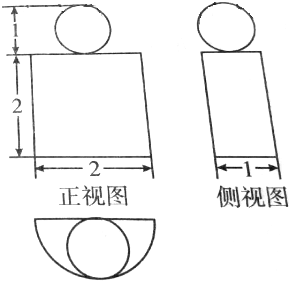

| A、该几何体的表面积为4+2π | ||
B、该几何体的体积为
| ||
| C、该几何体的表面积为4+4π | ||
| D、该几何体的体积为π |