题目内容
定义在(0,+∞)上的函数A满足:①当x∈[1,3)时,f(x)=1-|x-2|;②f(3x)=3f(x).设关于x的函数F(x)=f(x)-a的零点从小到大依次为x1,x2,…,xn,…,若a∈(1,3),则x1+x2+…+x2014= .
考点:函数的零点
专题:计算题,作图题,函数的性质及应用
分析:由题意可得,当x∈[3n-1,3n),(n∈N*)时,f(x)=3n-1-|x-2•3n-1|,作函数图象可得其和为6(31007-1).
解答:
解:当x∈[3n-1,3n),(n∈N*)时,
f(x)=3f(
)=32f(
)=…=3n-1f(
)
=3n-1[1-|
-2|]=3n-1-|x-2•3n-1|,
作函数f(x)的图象如下,
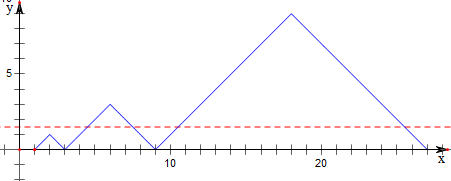
则其零点从小到大,
x1+x2=4×3,x3+x4=4×32,x2013+x2014=4×31007;
故x1+x2+…+x2014=4×(3+32+…+31007)
=6(31007-1);
故答案为:6(31007-1).
f(x)=3f(
| x |
| 3 |
| x |
| 32 |
| x |
| 3n-1 |
=3n-1[1-|
| x |
| 3n-1 |
作函数f(x)的图象如下,

则其零点从小到大,
x1+x2=4×3,x3+x4=4×32,x2013+x2014=4×31007;
故x1+x2+…+x2014=4×(3+32+…+31007)
=6(31007-1);
故答案为:6(31007-1).
点评:本题考查了函数的零点的应用,属于基础题.

练习册系列答案
相关题目
已知集合M={-1,1,2},N={x∈R|x2-5x+4=0},则M∪N=( )
| A、ϕ | B、{1} |
| C、{1,4} | D、{-1,1,2,4} |
函数f(x)=sinx在区间[a,b]上是增函数,且f(a)=-1,f(b)=1,则cos
的值为( )
| a+b |
| 2 |
| A、-1 | ||||
| B、0 | ||||
C、
| ||||
| D、1 |
在区间[0,2π]上任取一个数x,则使得2sinx>1的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
“所有9的倍数都是3的倍数,某奇数是9的倍数,故该奇数是3的倍数”,上述推理( )
| A、推理形式不正确 |
| B、大前提错误 |
| C、错误,因为大小前提不一致 |
| D、完全正确 |
