题目内容
已知△ABC的内角A,B,C所对的边分别是a,b,c,且b=3a;
(1)若C=
,△ABC的面积为
,求a的值;
(2)求
-4sin2
的值.
(1)若C=
| π |
| 3 |
3
| ||
| 4 |
(2)求
| sin(C-A) |
| sinA |
| C |
| 2 |
考点:正弦定理
专题:计算题,解三角形
分析:(1)根据题意,利用三角形的面积公式得到S△ABC=
absinC=
a2,由△ABC的面积为
建立关于a的等式,解之即可得到边a的值;
(2)根据b=3a利用正弦定理可得
=3,再由二倍角的余弦公式将原式化简,通分后再利用两角和与差的正弦加以计算,可得原式的值为1.
| 1 |
| 2 |
3
| ||
| 4 |
3
| ||
| 4 |
(2)根据b=3a利用正弦定理可得
| sinB |
| sinA |
解答:
解:(1)∵△ABC中,b=3a,C=
∴△ABC的面积为S=
absinC=
,
即
a2=
,解之得a=1;
(2)∵b=3a,∴由正弦定理得sinB=3sinA,可得
=3;
因此,
-4sin2
=
-2(1-cosC)
=
-2=
-2=
-2=
-2=1,
即
-4sin2
的值为1.
| π |
| 3 |
∴△ABC的面积为S=
| 1 |
| 2 |
3
| ||
| 4 |
即
3
| ||
| 4 |
3
| ||
| 4 |
(2)∵b=3a,∴由正弦定理得sinB=3sinA,可得
| sinB |
| sinA |
因此,
| sin(C-A) |
| sinA |
| C |
| 2 |
| sin(C-A) |
| sinA |
=
| sin(C-A)+2sinAcosC |
| sinA |
| sinCcosA+cosCsinA |
| sinA |
| sin(C+A) |
| sinA |
| sinB |
| sinA |
即
| sin(C-A) |
| sinA |
| C |
| 2 |
点评:本题给出三角形的边a、b的倍数关系,在已知角C与面积的情况下求边a的长,并求关于A、C的三角函数式的值.着重考查了和与差的三角函数公式、三角形的面积公式和正弦定理等知识,属于中档题.

练习册系列答案
相关题目
设a、b是非负实数,且a2+b2=4,则
( )
| ab |
| a+b+2 |
A、有最大值
| ||
B、有最小值
| ||
C、有最大值
| ||
D、有最小值
|
三个数208,351,429的最大公约数是( )
| A、65 | B、91 | C、26 | D、13 |
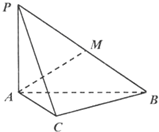 如图,三棱锥P-ABC中,∠ACB=90°,PA⊥底面ABC.
如图,三棱锥P-ABC中,∠ACB=90°,PA⊥底面ABC.