题目内容
某工厂生产某产品x吨所需费用P元,而卖出x吨的价格为每吨Q元,已知P=1000+5x+
x2,Q=a+
.
(1)试写出利润y关于x的函数;
(2)若生产出的产品能全部卖掉,且当产量为150吨时利润最大,此时每吨价格为40元,求实数a、b.
| 1 |
| 10 |
| x |
| b |
(1)试写出利润y关于x的函数;
(2)若生产出的产品能全部卖掉,且当产量为150吨时利润最大,此时每吨价格为40元,求实数a、b.
考点:根据实际问题选择函数类型
专题:应用题,函数的性质及应用
分析:(1)根据产品所获利润W=每吨售价Q元×吨数x-x吨需费用P元,建立函数关系式,
(2)利用当产量为150吨时利润最大,此时每吨价格为40元,建立方程,即可求实数a、b.
(2)利用当产量为150吨时利润最大,此时每吨价格为40元,建立方程,即可求实数a、b.
解答:
解:由题意得
(1)W=Qx-P=(a+
)x-(
x2+5x+1000)=(
-
)x2+(a-5)x-1000;
(2)∵当产量为150吨时利润最大,此时每吨价格为40元,
∴-
=150,
=40,
∴a=45,b=-30.
(1)W=Qx-P=(a+
| x |
| b |
| 1 |
| 10 |
| 1 |
| b |
| 1 |
| 10 |
(2)∵当产量为150吨时利润最大,此时每吨价格为40元,
∴-
| a-5 | ||||
2(
|
-4000(
| ||||
4(
|
∴a=45,b=-30.
点评:本题考查根据实际问题,列二次函数关系式解决实际应用题.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
相关题目
设函数f(x)、g(x)的定义域分别为F、G,且F⊆G.若对任意的x∈F,都有f(x)=g(x),则称g(x)为f(x)在G上的一个“延拓函数”.已知f(x)=2x(x≤0),若g(x)为f(x)在R上的一个延拓函数,且g(x)是偶函数,则g(x)的解析式是( )
| A、log2|x| | ||
| B、2|x| | ||
C、log
| ||
D、(
|
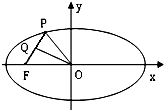 如图,P是椭圆
如图,P是椭圆 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图(第一个为正(主),下面的是俯视图)则该多面体的体积为.
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图(第一个为正(主),下面的是俯视图)则该多面体的体积为.