题目内容
对于任意给定的实数m，直线3x+y-m=0与双曲线
-
=1（a＞0，b＞0）最多有一个交点，则双曲线的离心率等于（ ）
| y2 |
| a2 |
| x2 |
| b2 |
A、
| ||||
B、
| ||||
| C、3 | ||||
D、2
|
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由题意可知，直线3x-y+m=0与双曲线的其中一条渐近线重合或平行，则有
=3，代入c2=a2+b2求出离心率．那么这条渐近线方程
| a |
| b |
解答：
解：由题意可知，直线3x-y+m=0与双曲线的其中一条渐近线重合或平行，
那么这条渐近线方程可写为：3x-y=0
即：y=3x
∵双曲线的焦点在y轴上，
则有
=3，即b=
那么：c2=a2+b2=
即：
=
解得：e=
=
故选A．
那么这条渐近线方程可写为：3x-y=0
即：y=3x
∵双曲线的焦点在y轴上，
则有
| a |
| b |
| a |
| 3 |
那么：c2=a2+b2=
| 10a2 |
| 9 |
即：
| c2 |
| a2 |
| 10 |
| 9 |
解得：e=
| c |
| a |
| ||
| 3 |
故选A．
点评：本题考查直线与双曲线的渐近线平行时与双曲线的交点最大一个，考查离心率的求法：即得到a，c的关系，属于中档题．
练习册系列答案
相关题目
已知点G是△ABC的重心，若A=
，
•
=3，则|
|的最小值为（ ）
| π |
| 3 |
| AB |
| AC |
| AG |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
已知甲盒中仅有1个球且为红球，乙盒中有m个红球和n个蓝球（m≥3，n≥3），从乙盒中随机抽取i（i=1，2）个球放入甲盒中．
（a）放入i个球后，甲盒中含有红球的个数记为ξi（i=1，2）；
（b）放入i个球后，从甲盒中取1个球是红球的概率记为pi（i=1，2）．
则（ ）
（a）放入i个球后，甲盒中含有红球的个数记为ξi（i=1，2）；
（b）放入i个球后，从甲盒中取1个球是红球的概率记为pi（i=1，2）．
则（ ）
| A、p1＞p2，E（ξ1）＜E（ξ2） |
| B、p1＜p2，E（ξ1）＞E（ξ2） |
| C、p1＞p2，E（ξ1）＞E（ξ2） |
| D、p1＜p2，E（ξ1）＜E（ξ2） |
设点（a，b）是区域
内的随机点，函数f（x）=ax2-4bx+1在区间[1，+∞）上是增函数的概率为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
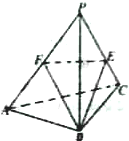如图：已知正三棱锥P-ABC，侧棱PA，PB，PC的长为2，且∠APB=30°，E，F分别是侧棱PC，PA上的动点，则△BEF的周长的最小值为（ ）A、8-4
| ||
| B、2 | ||
C、2
| ||
D、1+2
|
若不等式lg
≥（x-1）lg3对任意x∈（-∞，1）恒成立，则a的取值范围是（ ）
| 1+2x+(1-a)3x |
| 3 |
| A、（-∞，0] |
| B、[1，+∞） |
| C、[0，+∞） |
| D、（-∞，1] |
如图，三棱锥A-BCD中，AB⊥平面BCD，CD⊥BD．