题目内容
20．已知双曲线${x^2}-\frac{y^2}{3}=1$，过P（2，0）且倾斜角为30°的直线l与双曲线相交于A，B两点（1）写出直线l的参数方程．
（2）求|PA|+|PB|的值．
分析 （1）直线l的参数方程为：$\left\{\begin{array}{l}{x=2+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.（t为参数）$．
（2）易知倾斜角为30°的直线l与双曲线相交于A，B两点，A、B在异支，把直线l的参数方程为：$\left\{\begin{array}{l}{x=2+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.（t为参数）$．代入${x^2}-\frac{y^2}{3}=1$得：$2{t}^{2}+6\sqrt{3}t+9=0$，⇒${t}_{1}+{t}_{2}=-3\sqrt{3}$，${t}_{1}{t}_{2}=\frac{9}{2}$，|PA|+|PB|=|t1-t2|=3．
解答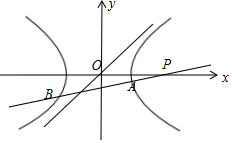 
解：（1）过P（2，0）且倾斜角为30°的直线l的参数方程为：$\left\{\begin{array}{l}{x=2+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.（t为参数）$．
（2）∵双曲线${x^2}-\frac{y^2}{3}=1$的渐近线为y=$\sqrt{3}$x，其倾斜角为600
∴倾斜角为30°的直线l与双曲线相交于A，B两点，A、B在异支．
把直线l的参数方程为：$\left\{\begin{array}{l}{x=2+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.（t为参数）$．代入${x^2}-\frac{y^2}{3}=1$得：
$2{t}^{2}+6\sqrt{3}t+9=0$，⇒${t}_{1}+{t}_{2}=-3\sqrt{3}$，${t}_{1}{t}_{2}=\frac{9}{2}$，
$（{t}_{1}-{t}_{2}）^{2}=（{t}_{1}+{t}_{2}）^{2}-4{t}_{1}{t}_{2}$=（-3$\sqrt{3}）^{2}$2-4×$\frac{9}{2}=9$．
|PA|+|PB|=|t1-t2|=3．
点评 本题考查了直线的参数方程，直线与双曲线的位置关系，解题时要注意参数的本质含义，属于中档题．
| A． | 等于0 | B． | 等于$\frac{π}{6}$ | C． | 等于$\frac{π}{2}$ | D． | 不存在 |
| A． | $\frac{{{3^{101}}-16203}}{2}$ | B． | $\frac{{{3^{100}}-15387}}{2}$ | C． | $\frac{{{3^{101}}-15387}}{2}$ | D． | $\frac{{{3^{100}}-16203}}{2}$ |