题目内容
12.将3个小球随机地投入编号为1,2,3,4的4个小盒中(每个盒子容纳的小球的个数没有限制),则1号盒子中小球的个数ξ的期望为$\frac{3}{4}$.分析 将3个小球随机地投入编号为1,2,3,4的4个小盒中,每个小球有4种不同的放法,共有43种;
1号盒子中小球的个数ξ的可能取值为0,1,2,3;求出对应的概率值,
写出随机变量ξ的分布列,计算数学期望值.
解答 解:将3个小球随机地投入编号为1,2,3,4的4个小盒中,
每个小球有4种不同的放法,共有43=64种;
则1号盒子中小球的个数ξ的可能取值为0,1,2,3;
且P(ξ=0)=$\frac{{3}^{3}}{{4}^{3}}$=$\frac{27}{64}$,
P(ξ=1)=$\frac{{C}_{3}^{1}{•3}^{2}}{{4}^{3}}$=$\frac{27}{64}$,
P(ξ=2)=$\frac{{C}_{3}^{2}•3}{{4}^{3}}$=$\frac{9}{64}$,
P(ξ=3)=$\frac{{C}_{3}^{3}{•3}^{0}}{{4}^{3}}$=$\frac{1}{64}$;
则随机变量ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{27}{64}$ | $\frac{27}{64}$ | $\frac{9}{64}$ | $\frac{1}{64}$ |
点评 本题考查了离散型随机变量的分布列与数学期望的应用问题,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知直线l:4x+3y-20=0经过双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的一个焦点,且与其一条渐近线平行,则双曲线C的实轴长为( )
| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
2.下列求导正确的是( )
| A. | (3x2-2)'=3x | B. | (log2x)'=$\frac{1}{x•ln2}$ | C. | (cosx)'=sinx | D. | ($\frac{1}{lnx}$)'=x |
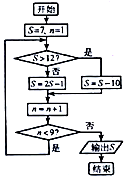 阅读如图的程序框图,运行相应的程序,则输出的S值为3.
阅读如图的程序框图,运行相应的程序,则输出的S值为3.