题目内容
9.已知函数f(x)=xex-a(x-1)(a∈R)(1)若函数f(x)在x=0处有极值,求a的值及f(x)的单调区间
(2)若存在实数x0∈(0,$\frac{1}{2}$),使得f(x0)<0,求实数a的取值范围.
分析 (1)求出函数的导数,求出a的值,解关于导函数的不等式,求出函数的单调区间即可;
(2)问题转化为a<$\frac{{xe}^{x}}{x-1}$在x∈(0,$\frac{1}{2}$)上有解,设h(x)=$\frac{{xe}^{x}}{x-1}$,x∈(0,$\frac{1}{2}$),根据函数的单调性求出a的范围即可.
解答 解:(1)f′(x)=(x+1)ex-a,
由f′(0)=0,解得:a=1,
故f′(x)=(x+1)ex-1,
令f′(x)>0,解得:x>0,令f′(x)<0,解得:x<0,
故f(x)在(-∞,0)递减,在(0,+∞)递增;
(2)若f(x)<0在x∈(0,$\frac{1}{2}$)上有解,
即xex<a(x-1),a<$\frac{{xe}^{x}}{x-1}$在x∈(0,$\frac{1}{2}$)上有解,
设h(x)=$\frac{{xe}^{x}}{x-1}$,x∈(0,$\frac{1}{2}$),
则h′(x)=$\frac{{e}^{x}{(x}^{2}-x-1)}{{(x-1)}^{2}}$<0,
故h(x)在(0,$\frac{1}{2}$)递减,
h(x)在(0,$\frac{1}{2}$)的值域是(-$\sqrt{e}$,0),
故a<h(0)=0.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查转化思想,是一道中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
20.已知函数f(x)=ax2+bx+c,且a>b>c,a+b+c=0,集合A={m|f(m)<0},则( )
| A. | 任意m∈A,都有f(m+3)>0 | B. | 任意m∈A,都有f(m+3)<0 | ||
| C. | 存在m∈A,都有f(m+3)=0 | D. | 存在m∈A,都有f(m+3)<0 |
1.已知直线l:4x+3y-20=0经过双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的一个焦点,且与其一条渐近线平行,则双曲线C的实轴长为( )
| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
19.命题“?x0∈R,$\frac{2}{x_0}$+lnx0≥0”的否定是( )
| A. | $?{x}∈R,\frac{2}{x}+ln{x}<0$ | B. | $?{x}∈R,\frac{2}{x}+ln{x}≤0$ | ||
| C. | $?{x_0}∈R,\frac{2}{x_0}+ln{x_0}<0$ | D. | $?{x_0}∈R,\frac{2}{x_0}+ln{x_0}≤0$ |
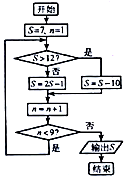 阅读如图的程序框图,运行相应的程序,则输出的S值为3.
阅读如图的程序框图,运行相应的程序,则输出的S值为3.