题目内容
2.函数f(x)=$\frac{\sqrt{1-{x}^{2}}}{x+3}$-m有零点,则实数m的取值范围是多少?分析 先求出函数的导数,得出函数的单调性,从而求出函数的最值,进而求出m的范围.
解答 解:∵f′(x)=-$\frac{3x+1}{\sqrt{1-{x}^{2}}•(x+3)^{2}}$,
令f′(x)>0,解得:x<-$\frac{1}{3}$,
令f′(x)<0,解得:x>-$\frac{1}{3}$,
又1-x2≥0,
∴-1≤x≤1,
∴f(x)在[-1,-$\frac{1}{3}$)递增,在(-$\frac{1}{3}$,1]递减,
∴f(x)max=f(-$\frac{1}{3}$)=$\frac{\sqrt{2}}{4}$-m,f(x)min=f(1)=0-m,
∴m的范围是[0,$\frac{\sqrt{2}}{4}$].
点评 本题考查了函数的零点问题,考查转化思想,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知函数f(x)=|log2|x||-($\frac{1}{2}$)x,则下列结论正确的是( )
| A. | f(x)有三个零点,且所有零点之积大于-1 | |
| B. | f(x)有三个零点,且所有零点之积小于-1 | |
| C. | f(x)有四个零点,且所有零点之积大于1 | |
| D. | f(x)有四个零点,且所有零点之积小于1 |
17.已知$\frac{1}{2}$<a<4,函数f(x)=x3-3bx2+a有且仅有两个不同的零点x1,x2,则|x1-x2|的取值范围是( )
| A. | ($\frac{1}{2}$,1) | B. | (1,2) | C. | ($\frac{3}{2}$,3) | D. | (2,3) |
14.已知A(1,-2,11),B(6,-1,4),C(4,2,3),则△ABC为( )
| A. | 锐角三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 钝角三角形 |
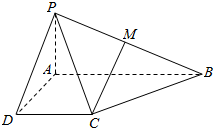 如图,在四棱锥P-ABCD中,已AB∥CD,AB=2DC,M为PB的中点.
如图,在四棱锥P-ABCD中,已AB∥CD,AB=2DC,M为PB的中点.