题目内容
15.抛物线经过点(2,-3),它与x轴交点的横坐标是-1和3.(1)求出抛物线的解析式;
(2)用配方法求出抛物线的对称轴和顶点坐标;
(3)画出草图;
(4)观察图象,x取何值时,函数值y小于零?x取何值时,y随x的增大而减小?
分析 (1)设抛物线的解析式为y=a(x+1)(x-3)(a≠0),把点(2,-3)代入,得解析式;
(2)把解析式化为顶点式求顶点坐标和对称轴;
(3)根据(2)画出草图;
(4)依据图象可知,当图象在x轴下方时,y<0,在对称轴的左边,y随x的增大而减小.
解答 解:(1)设抛物线的解析式为y=a(x+1)(x-3)(a≠0),
把点(2,-3)代入,得-3=a(2+1)(2-3),∴a=1.
∴抛物线的解析式为y=(x+1)(x-3)=x2-2x-3.
(2)y=x2-2x-3=(x-1)2-4.
由此可知抛物线的对称轴方程为x=1,顶点坐标为(1,-4).
(3)抛物线的草图如图所示: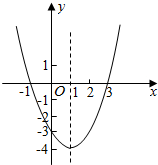
(4)由图象可知,当x∈(-1,3)时,函数值y小于零;
当x∈(-∞,1]时,y随x的增大而减小.
点评 主要考查了用待定系数法求二次函数的解析式和二次函数及其图象的性质.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
5.已知抛物线的顶点在原点,焦点在y轴上,其上的点P(m,-3)到焦点的距离为5,則抛物线方程为( )
| A. | x2=8y | B. | x2=4y | C. | x2=-4y | D. | x2=-8y |
6.某工厂从1970年的年产值200万元增加到40年后2010年的1000万元,假设每年产值增长率相同,则每年年产值增长率是(x为很小的正数时,ln(1+x)≈x,ln5≈1.61)( )
| A. | 3% | B. | 4% | C. | 5% | D. | 6% |
10.已知函数f(x)=|log2|x||-($\frac{1}{2}$)x,则下列结论正确的是( )
| A. | f(x)有三个零点,且所有零点之积大于-1 | |
| B. | f(x)有三个零点,且所有零点之积小于-1 | |
| C. | f(x)有四个零点,且所有零点之积大于1 | |
| D. | f(x)有四个零点,且所有零点之积小于1 |
20.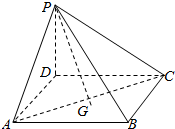 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,ABCD为正方形,且PD=AB=1,G为△ABC的重心,则PG与底面所成的角θ满足( )
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,ABCD为正方形,且PD=AB=1,G为△ABC的重心,则PG与底面所成的角θ满足( )
 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,ABCD为正方形,且PD=AB=1,G为△ABC的重心,则PG与底面所成的角θ满足( )
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,ABCD为正方形,且PD=AB=1,G为△ABC的重心,则PG与底面所成的角θ满足( )| A. | θ=$\frac{π}{4}$ | B. | cosθ=$\frac{2\sqrt{34}}{17}$ | C. | tanθ=$\frac{2\sqrt{2}}{3}$ | D. | sinθ=$\frac{\sqrt{3}}{3}$ |
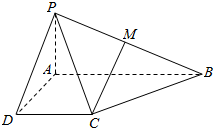 如图,在四棱锥P-ABCD中,已AB∥CD,AB=2DC,M为PB的中点.
如图,在四棱锥P-ABCD中,已AB∥CD,AB=2DC,M为PB的中点.