题目内容
16.已知Rt△ABC中,∠C=90°.AC=3,BC=4,P为线段AB上的点,且$\overrightarrow{CP}$=$\frac{x}{|\overrightarrow{CA}|}$•$\overrightarrow{CA}$+$\frac{y}{|\overrightarrow{CB}|}$•$\overrightarrow{CB}$,则xy的最大值为( )| A. | 3 | B. | 2 | C. | 1 | D. | 4 |
分析 根据三点共线的向量式子,得出x与y的关系.根据基本不等式得出xy的最大值.
解答 解:P为线段AB上的点,且$\overrightarrow{CP}$=$\frac{x}{|\overrightarrow{CA}|}$•$\overrightarrow{CA}$+$\frac{y}{|\overrightarrow{CB}|}$•$\overrightarrow{CB}$.
∴$\frac{x}{|\overrightarrow{CA}|}+\frac{y}{|\overrightarrow{BC}|}$=$\frac{x}{3}+\frac{y}{4}=1$且x>0,y>0
∴$\frac{x}{3}+\frac{y}{4}≥2\sqrt{\frac{x}{3}•\frac{y}{4}}=\sqrt{\frac{xy}{3}}$
∴xy≤3
当且仅当$\frac{x}{3}=\frac{y}{4}$时,等号成立.
则xy的最大值为3.
故选:A.
点评 考查平面向量三点共线问题,基本不等式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知x,y满足约束条件$\left\{\begin{array}{l}2x+y-2≥0\\ x-2y+4≥0\\ 3x-y-3≤0\end{array}\right.$,目标函数z=x2+y2的最大值为( )
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{4}{5}$ | C. | $\sqrt{13}$ | D. | 13 |
4.执行如图所示的程序框图,若$a=\frac{9}{4}$,则输出S的值为( )
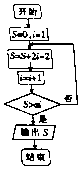

| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
11.点(2,0,3)位于( )
| A. | Y轴上 | B. | X轴上 | C. | XOZ平面内 | D. | YOZ平面内 |
1.曲线M的方程为$\sqrt{{{(x-1)}^2}+{y^2}}+\sqrt{{{(x+1)}^2}+{y^2}}$=4,直线y=k(x+1)交曲线M于A,B两点,点C(1,0),则△ABC的周长为( )
| A. | 4 | B. | $4\sqrt{2}$ | C. | $4\sqrt{3}$ | D. | 8 |
8.A,B,C是球O上的三点,AB=5,AC=3,BC=4,球O的直径等于13,则球心O到平面ABC的距离为( )
| A. | $2\sqrt{3}$ | B. | 6 | C. | 9 | D. | 12 |
6.抛物线x2=-8y的通径为线段AB,O为抛物线的顶点,则通径长和△AOB的面积分别是( )
| A. | 4,4 | B. | 4,2 | C. | 8,8 | D. | 8,4 |