题目内容

7．已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=x2-x，求f（x）的解析式．

分析 根据函数的奇偶性，设x＜0时，则-x＞0，得到f（-x）=x2+x，求出函数的解析式即可．

解答 解：由已知得f（0）=0，当x＜0时，
则-x＞0，而x＞0时，
f（x）=x2-x，所以f（-x）=x2+x，
又f（x）为奇函数，所以f（x）=-f（-x），
所以得f（x）=-x2-x，
综上可知f（x）=$\left\{\begin{array}{l}{{-x}^{2}-x，x＜0}\\{0，x=0}\\{{x}^{2}-x，x＞0}\end{array}\right.$．

点评 本题考查了求函数的解析式问题，考查函数的奇偶性，是一道基础题．

练习册系列答案
相关题目
17．在△ABC中，角A、B、C的对边分别为a，b，c，且满足a2-b2-c2+$\sqrt{3}$bc=0，2bsinA=a，BC边上中线AM的长为$\sqrt{14}$
（ I）求角A和角B的大小；
（ II）求△ABC的各边长．
18．若$α∈（\frac{π}{2}，π）$，则$\frac{3}{2}cos2α=sin（\frac{π}{4}-α）$，则sin2α的值为（　　）
A．$\frac{2}{9}$B．$-\frac{2}{9}$C．$\frac{7}{9}$D．$-\frac{7}{9}$
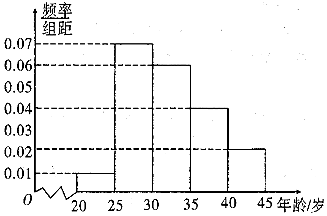15．“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称，某市为了了解人们对“一带一路”的认知程度，对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛，满分100分（90分及以上为认知程度高），现从参赛者中抽取了x人，按年龄分成5组（第一组：[20，25），第二组：[25，30），第三组：[30，35），第四组：[35，40），第五组：[40，45]），得到如图所示的频率分布直方图，已知第一组有6人．
（1）求x；
（2）求抽取的x人的年龄的中位数（结果保留整数）；
（3）从该市大学生、军人、医务人员、工人、个体户五种人中用分层抽样的方法依次抽取6人，42人，36人，24人，12人，分别记1～5组，从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛代表相应的成绩，年龄组中1～5组的成绩分别为93，96，97，94，90，职业组中1～5组的成绩分别为93，98，94，95，90．
（I）分别求5个年龄组和5个职业组成绩的平均数和方差；
（II）以上述数据为依据，评价5个年龄组和5个职业组对“一带一路”的认知程度，并谈谈你的感想．
2．已知公比小于1的等比数列{an}的前n项和为Sn，a1=$\frac{1}{2}，7{a_2}=2{S_3}$．
（1）求数列{an}的通项公式；
（2）设bn=log2（1-Sn+1），若$\frac{1}{{{b_1}{b_3}}}+\frac{1}{{{b_3}{b_5}}}+…+\frac{1}{{{b_{2n-1}}{b_{2n+1}}}}=\frac{5}{21}$，求n．
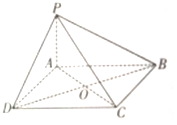12．如图所示，四棱锥P-ABCD中，底面ABCD为平行四边形，PA⊥AD，PA⊥AB，AB=AD，AC与BD交于点O．
（Ⅰ）求证：平面PAC⊥平面PBD；
（Ⅱ）直线PD与过直线AC的平面α平行，平面α与棱PB交于点M，指明点M的位置，并证明．
19．sin（π-α）=$\frac{1}{7}$，α是第二象限角，则tanα=$\frac{\sqrt{3}}{12}$．
16．已知Rt△ABC中，∠C=90°．AC=3，BC=4，P为线段AB上的点，且$\overrightarrow{CP}$=$\frac{x}{|\overrightarrow{CA}|}$•$\overrightarrow{CA}$+$\frac{y}{|\overrightarrow{CB}|}$•$\overrightarrow{CB}$，则xy的最大值为（　　）
A．3B．2C．1D．4
17．在等比数列{an}中，S3=3a3，则其公比q的值为（　　）
A．-$\frac{1}{2}$B．$\frac{1}{2}$C．1或-$\frac{1}{2}$D．-1或$\frac{1}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网