题目内容
1.曲线M的方程为$\sqrt{{{(x-1)}^2}+{y^2}}+\sqrt{{{(x+1)}^2}+{y^2}}$=4,直线y=k(x+1)交曲线M于A,B两点,点C(1,0),则△ABC的周长为( )| A. | 4 | B. | $4\sqrt{2}$ | C. | $4\sqrt{3}$ | D. | 8 |
分析 直线经过定点(-1,0),由椭圆定义,转化求解△ABM的周长即可.
解答 解:曲线M的方程为$\sqrt{{{(x-1)}^2}+{y^2}}+\sqrt{{{(x+1)}^2}+{y^2}}$=4,可知(±1,0)是椭圆的焦点,由椭圆定义知:2a=4,直线y=k(x+1)过定点(-1,0),
由题设△ABC的周长为AB+BC+AC=4a=8,
故选:D.
点评 本题考查椭圆的定义,直线经过定点问题,直线和圆锥曲线的关系,利用椭圆的定义是解题的关键,属于中档题.

练习册系列答案
相关题目
11. 某校高三期中考试后,数学教师对本次全部数学成绩按1:20进行分层抽样,随机抽取了20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如表所示的频率分布表:
某校高三期中考试后,数学教师对本次全部数学成绩按1:20进行分层抽样,随机抽取了20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如表所示的频率分布表:
(Ⅰ)求表中a,b,c的值,并估计这次考试全校高三数学成绩的及格率(成绩在[90,150]内为及格);
(Ⅱ)设茎叶图中成绩在[100,120)范围内的样本的中位数为m,若从成绩在[100,120)范围内的样品中每次随机抽取1个,每次取出不放回,连续取两次,求取出两个样本中恰好一个是数字m的概率.
 某校高三期中考试后,数学教师对本次全部数学成绩按1:20进行分层抽样,随机抽取了20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如表所示的频率分布表:
某校高三期中考试后,数学教师对本次全部数学成绩按1:20进行分层抽样,随机抽取了20名学生的成绩为样本,成绩用茎叶图记录如图所示,但部分数据不小心丢失,同时得到如表所示的频率分布表:| 分数段 | [50,70) | [70,90) | [90,110) | [110,130) | [130,150] | 总计 |
| 频数 | c | b | ||||
| 频率 | a |
(Ⅱ)设茎叶图中成绩在[100,120)范围内的样本的中位数为m,若从成绩在[100,120)范围内的样品中每次随机抽取1个,每次取出不放回,连续取两次,求取出两个样本中恰好一个是数字m的概率.
9.从甲、乙、丙等5名候选学生中选出2名作为校运动会志愿者,则甲、乙、丙中有2人被选中的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{10}$ | C. | $\frac{3}{20}$ | D. | $\frac{1}{20}$ |
6.若a=20.1,b=ln2,c=log0.36,则a,b,c的大小关系为( )
| A. | a>c>b | B. | c>b>a | C. | a>b>c | D. | b>c>a |
10.球的大圆面积扩大为原大圆面积的4倍,则球的表面积扩大成原球表面积的( )
| A. | 2倍 | B. | 4倍 | C. | 8倍 | D. | 16倍 |
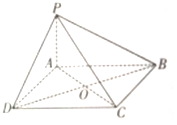 如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥AD,PA⊥AB,AB=AD,AC与BD交于点O.
如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥AD,PA⊥AB,AB=AD,AC与BD交于点O.