题目内容
4.设实数x,y满足约束条件$\left\{\begin{array}{l}{x-y-2≤0}\\{x+y-2≤0}\\{x≥-2}\end{array}\right.$,则x2+(y+4)2的取值范围是( )| A. | [2,68] | B. | [4,68] | C. | [2,2$\sqrt{17}$] | D. | [$\sqrt{2}$,2$\sqrt{17}$] |
分析 由题意作平面区域,而x2+(y+4)2的几何意义是点A(0,-4)与阴影内的点的距离的平方,从而结合图象解得.
解答 解:由题意作$\left\{\begin{array}{l}{x-y-2≤0}\\{x+y-2≤0}\\{x≥-2}\end{array}\right.$平面区域如下,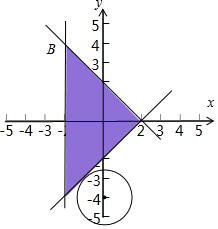 ,
,
x2+(y+4)2的几何意义是点A(0,-4)与阴影内的点的距离的平方,
而点A到直线x-y-2=0的距离d=$\frac{|2-4|}{\sqrt{2}}$=$\sqrt{2}$,由$\left\{\begin{array}{l}{x=-2}\\{x+y-2=0}\end{array}\right.$
B(-2,4),故|AB|=$\sqrt{({-2)}^{2}+(4+4)^{2}}$=$\sqrt{68}$,
故($\sqrt{2}$)2≤x2+(y+2)2≤($\sqrt{68}$)2,
即2≤x2+(y+2)2≤68,
故选:A.
点评 本题考查了线性规划的变形应用及数形结合的思想应用,同时考查了转化思想的应用.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
14.在圆(x-1)2+(y-3)2=25内过点(1,0)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
| A. | 40 | B. | 20 | C. | 80 | D. | 10 |
15.已知等比数列{an}中,a2a10=6a6,等差数列{bn}中,b4+b6=a6,则数列{bn}的前9项和为( )
| A. | 9 | B. | 27 | C. | 54 | D. | 72 |
12.设F1、F2是椭圆$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{2}$=1的两个焦点,点P在椭圆上,当△F1PF2的面积为2时,$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}$=( )
| A. | -$\frac{2\sqrt{6}}{3}$ | B. | 0 | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
19.已知角α的终边经过点P(-1,2),则tanα的值是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
2.若曲线C1:y=ax2(a>0)与曲线C2:y=e-x有公共切线,则a的取值范围为( )
| A. | [$\frac{{e}^{2}}{4}$,+∞) | B. | [$\frac{{e}^{2}}{8}$,+∞) | C. | (0,$\frac{{e}^{2}}{4}$] | D. | (0,$\frac{{e}^{2}}{8}$] |
3.已知随机变量X的概率分布如下:
则V(X)=1.01.
| X | 1 | 2 | 3 | 4 |
| P | 0.1 | 0.4 | 0.2 | 0.3 |