题目内容
2．若曲线C1：y=ax2（a＞0）与曲线C2：y=e-x有公共切线，则a的取值范围为（ ）| A． | [$\frac{{e}^{2}}{4}$，+∞） | B． | [$\frac{{e}^{2}}{8}$，+∞） | C． | （0，$\frac{{e}^{2}}{4}$] | D． | （0，$\frac{{e}^{2}}{8}$] |
分析 求出两个函数的导函数，由导函数相等列方程，再由方程有根转化为两函数图象有交点求得a的范围．
解答 解：设公切线与曲线C1切于点（x1，ax12），与曲线C2切于点（x2，${e}^{-{x}_{2}}$），
则曲线C1的导数为y′=2ax，C2的导数为y′=-e-x．
则2ax1=-${e}^{-{x}_{2}}$=$\frac{{e}^{-{x}_{2}}-a{{x}_{1}}^{2}}{{x}_{2}-{x}_{1}}$，
将${e}^{-{x}_{2}}$=-2ax1代入2ax1=$\frac{{e}^{-{x}_{2}}-a{{x}_{1}}^{2}}{{x}_{2}-{x}_{1}}$，可得2x2=x1-2，
∴a=-$\frac{{e}^{-\frac{{x}_{1}}{2}+1}}{2{x}_{1}}$，
记f（x）=-$\frac{{e}^{-\frac{x}{2}+1}}{2x}$，
则f′（x）=$\frac{{e}^{-\frac{x}{2}+1}（x+2）}{4{x}^{2}}$，当x∈（-∞，-2）时，f′（x）＜0．
当x∈（-2，+∞）时，f′（x）＞0，
∴当x=-2时，f（x）min=f（-2）=$\frac{{e}^{2}}{4}$．
∴a的范围是[$\frac{{e}^{2}}{4}$，+∞）．
故选A．
点评 本题考查了利用导数研究过曲线上某点处的切线方程，综合考查导数的应用，综合性较强，难度较大．
练习册系列答案
相关题目
4．设实数x，y满足约束条件$\left\{\begin{array}{l}{x-y-2≤0}\\{x+y-2≤0}\\{x≥-2}\end{array}\right.$，则x2+（y+4）2的取值范围是（ ）
| A． | [2，68] | B． | [4，68] | C． | [2，2$\sqrt{17}$] | D． | [$\sqrt{2}$，2$\sqrt{17}$] |
17．函数f（x）=sin（ωx+$\frac{π}{6}$）（ω＞0）的图象与x轴的交点横坐标构成一个公差为$\frac{π}{2}$的等差数列，要得到g（x）=cos（ωx+$\frac{π}{6}$）的图象，可将f（x）的图象（ ）
| A． | 向右平移$\frac{π}{4}$个单位 | B． | 向左平移$\frac{π}{4}$个单位 | ||
| C． | 向左平移$\frac{π}{2}$个单位 | D． | 向右平移$\frac{π}{2}$个单位 |
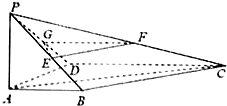已知如图，四边形ABCD是直角梯形，AB∥DC，AB⊥AD，AP⊥平面ABCD，DC=2AB=2AD=2AP，点E、F、G分别是PB、PC、PD的中点．