题目内容
已知平面向量
，
满足|
|=3，|
|=2，
与
的夹角为120°，若（
+m
）⊥
，则实数m的值为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、3 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由（
+mb
）⊥
，可得（
+m
）•
=0，再利用数量积的运算和定义展开即可得出．
| a |
| b |
| a |
| a |
| b |
| a |
解答：
解：∵|
|=3，|
|=2，
与
的夹角为120°，
∴
•
=|
| |
|cos120°=3×2×(-
)=-3．
∵（
+mb
）⊥
，
∴（
+m
）•
=
2+m
•
=32-3m=0，解得m=3．
故选：D．
| a |
| b |
| a |
| b |
∴
| a |
| b |
| a |
| b |
| 1 |
| 2 |
∵（
| a |
| b |
| a |
∴（
| a |
| b |
| a |
| a |
| a |
| b |
故选：D．
点评：本题考查了数量积的运算和定义、向量垂直与数量积的关系，属于基础题．
练习册系列答案
相关题目
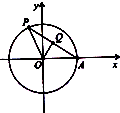如图，A是单位圆与x轴正半轴的交点，点P在该单位圆上，∠AOP=θ（0＜θ＜π），点Q满足| PQ |
| QA |
| OA |
| OQ |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若102x=25，则x=（ ）
A、lg
| ||
| B、lg5 | ||
| C、2lg5 | ||
D、2lg
|
已知等边三角形的边长为4，那么它水平放置的直观图的面积为（ ）
A、
| ||
| B、2 | ||
C、
| ||
| D、1 |
已知命题p：x=1是方程x+1=0的根；q：对于任意x∈R，总有|x|≥0，则下列命题为真命题的是（ ）
| A、p∧q | B、￢p∧￢q |
| C、p∧￢q | D、￢p∧q |
已知
，
是夹角为60°的两个单位向量，则
=2
+
与
=-3
+2
的夹角的正弦值是（ ）
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
复数z=3-2i所对应的点位于复平面的（ ）
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
若抛物线y2=4x的焦点是F，准线是l，则经过点F、M（4，4）且与l相切的圆共有（ ）
| A、4个 | B、2个 | C、1个 | D、0个 |
如图，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，且△ABC为正三角形，AA1=AB=6，D为AC的中点．