Question

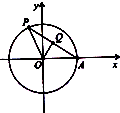如图，A是单位圆与x轴正半轴的交点，点P在该单位圆上，∠AOP=θ（0＜θ＜π），点Q满足

PQ

=

QA

，三角形OAP的面积记为S．则

OA

•

OQ

+S的最大值是（　　）

• A、

  2

  4

• B、

  2 +1

  2

• C、

  2

  2

• D、

  2 +1

  4

Answer 1

考点：平面向量数量积的运算

专题：平面向量及应用

分析：由题意可得，Q是线段PA的中点，OQ⊥PA，∠AOQ=

θ

2

∈（0，

π

2

），分别求得S和

OA

•

OQ

的值，利用三角恒等变换可得

OA

•

OQ

+S=

2

2

sin（θ+

π

4

）+

1

2

，由此可得

OA

•

OQ

+S的最大值．

解答： 解：由题意可得，Q是线段PA的中点，∴OQ⊥PA，∠AOQ=

θ

2

∈（0，

π

2

），
∴S=

1

2

•OA•OP•sinθ=

1

2

sinθ，

OA

•

OQ

=OA•OQ•cos

θ

2

=OQ²=cos2

θ

2

．
∴

OA

•

OQ

+S=cos2

θ

2

+

1

2

sinθ=

1

2

（cosθ+sinθ）+

1

2

=

2

2

sin（θ+

π

4

）+

1

2

，
故当θ=

π

4

时，

OA

•

OQ

+S取得最大值为

2 +1

2

，
故选：B．

点评：本题主要考查两个向量的数量积的定义，三角恒等变换，直角三角形中的边角关系，属于基础题．