题目内容
20.已知数列{an}的前n项和为Sn,Sn=2an-3n,(n∈N+)(1)求a1,a2;
(2)求证:数列{an+3}成等比数列;
(3)求数列{an}的通项公式an;
(4)数列{an}中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
分析 (1)根据递推公式,代值计算即可,
(2)根据an+1=Sn+1-Sn,求得an+1+3=2(an+3),判断出数列{an+3}是等比数列,
(3)利用等比数列的通项公式求得an+3进而求得an.
(4)设存在s,p,r∈N*,且s<p<r,使得as,ap,ar成等差数列,根据等差中项的性质可知2ap=as+ar,利用(1)中的an展开得2p+1=2s+2r,2p-s+1=1+2r-s,进而根据2p-s+1,2r-s为偶数,而1+2r-s为奇数,判断出假设不成立.故可知不存在这样的三项.
解答 解:(1)因为Sn=2an-3n,
当n=1时,S1=2a1-3,解得a1=3,
当n=2时,S2=2a2-3,解得a2=6,
(2)因为Sn=2an-3n,
所以Sn+1=2an+1-3(n+1),
则an+1=2an+1-2an-3,
所以an+1=2an+3,
所以an+1+3=2(an+3)
数列{an+3}是等比数列,
(3)由(2)知,数列{an+3}是等比数列,
因为a1+3=6,
所以an+3=6•2n-1=3•2n,
所以an=3•2n-3.
(4)设存在s,p,r∈N*,且s<p<r,使得as,ap,ar成等差数列,
则2ap=as+ar,即2(3•2p-3)=3•2s-3+3•2r-3
即2p+1=2s+2r,2p-s+1=1+2r-s,2p-s+1,2r-s为偶数,而1+2r-s为奇数,
所以2p+1=2s+2r不成立,故不存在满足条件的三项.
点评 题考查数列的通项公式的求法,探索数列{an}中是否存在三项成等差数列.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.

练习册系列答案
相关题目
15.定义在R上的偶函数f(x)在(-∞,0)上单调递增,设a=f(3),$b=f(-\sqrt{2})$,c=f(2),则a,b,c大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |
5.已知球O的一个内接三棱锥P-ABC,其中△ABC是边长为2的正三角形,PC为球O的直径,且PC=4,则此三棱锥的体积为( )
| A. | $\frac{2}{3}\sqrt{3}$ | B. | $\frac{4}{3}\sqrt{2}$ | C. | $\frac{4}{3}\sqrt{6}$ | D. | $\frac{2}{3}\sqrt{6}$ |
9.已知点A是抛物线C:x2=2py(p>0)上一点,O为坐标原点,若以点M(0,8)为圆心,|OA|的长为半径的圆交抛物线C于A,B两点,且△ABO为等边三角形,则p的值是( )
| A. | $\frac{3}{8}$ | B. | 2 | C. | 6 | D. | $\frac{2}{3}$ |
10.已知$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(2,m),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{b}$|=( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
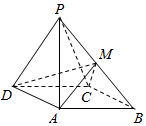 如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.
如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.