题目内容
12.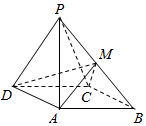 如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.
如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为$2\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.(1)求证:PA⊥CD;
(2)求三棱锥A-CDM的体积.
分析 (1)由已知结合面与面垂直的性质可得CD⊥平面APO,再由线面垂直的定义得到PA⊥CD;
(2)由题意求得P到底面的距离,然后把三棱锥A-CDM的体积转化为三棱锥M-ACD的体积求解.
解答 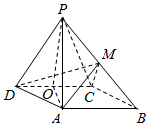 (1)证明:取DC的中点O,连接OP,OA,由△PDC是正三角形,有PO⊥DC
(1)证明:取DC的中点O,连接OP,OA,由△PDC是正三角形,有PO⊥DC
在菱形ABCD中,由于∠ADC=60°,$AD=2\sqrt{3}$,$OD=\sqrt{3}$,有AO⊥CD.
又PO⊥CD,OA∩OP=O,
则CD⊥平面APO,PA?平面APC,
即CD⊥PA;
(2)解:∵PO⊥CD,平面PCD⊥平面ABCD,
∴PO⊥底面ABCD,
∵PDC是正三角形,且PD=$2\sqrt{3}$,∴PO=$\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}=3$.
∵M是PB的中点,∴M到底面ABCD的距离$h=\frac{1}{2}PO=\frac{3}{2}$,
${V_{A-CDM}}={V_{M-ACD}}=\frac{1}{3}•{S_{△ACD}}•h=\frac{1}{3}×\frac{{\sqrt{3}}}{4}{({2\sqrt{3}})^2}×\frac{3}{2}=\frac{{3\sqrt{3}}}{2}$.
点评 本题考查平面与平面垂直的性质,考查了多面体体积的求法,训练了等积法,是中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
4.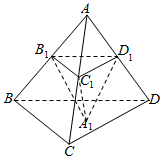 如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )
如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )
 如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )
如图,在棱长为a(a>0)的正四面体ABCD中,点B1,C1,D1分别在棱AB,AC,AD上,且平面B1C1D1∥平面BCD,A1为△BCD内一点,记三棱锥A1-B1C1D1的体积V,设$\frac{A{D}_{1}}{AD}$=x,对于函数V=f(x),则( )| A. | 当x=$\frac{2}{3}$时,函数f(x)取到最大值 | |
| B. | 函数f(x)在($\frac{1}{2}$,1)上是减函数 | |
| C. | 函数f(x)的图象关于直线x=$\frac{1}{2}$对称 | |
| D. | 存在x0,使得f(x0)$>\frac{1}{3}{V}_{A-BCD}$(其中VA-BCD为四面体ABCD的体积) |
2.设命题p:函数y=-xsinx的图象关于原点对称,
命题q:函数y=-xsinx在区间[0,$\frac{π}{2}$]上单调递减,
则下列命题中正确的是( )
命题q:函数y=-xsinx在区间[0,$\frac{π}{2}$]上单调递减,
则下列命题中正确的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
 如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充.已知金字塔的每一条棱和边都相等
如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充.已知金字塔的每一条棱和边都相等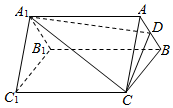 如图,已知三棱柱ABC-A1BlC1中,点D是AB的中点,平面A1DC分此棱柱成两部分,多面体A1ADC与多面体A1B1C1DBC体积的比值为1:5.
如图,已知三棱柱ABC-A1BlC1中,点D是AB的中点,平面A1DC分此棱柱成两部分,多面体A1ADC与多面体A1B1C1DBC体积的比值为1:5.