题目内容
5.已知球O的一个内接三棱锥P-ABC,其中△ABC是边长为2的正三角形,PC为球O的直径,且PC=4,则此三棱锥的体积为( )| A. | $\frac{2}{3}\sqrt{3}$ | B. | $\frac{4}{3}\sqrt{2}$ | C. | $\frac{4}{3}\sqrt{6}$ | D. | $\frac{2}{3}\sqrt{6}$ |
分析 取△ABC的中心E,则OE⊥平面ABC,所以P到平面ABC的距离h=2OE,利用正三角形的性质和勾股定理求出OE,代入棱锥的体积公式计算.
解答 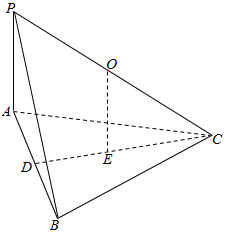 解:设△ABC的中心为E,AB中点为D,连结OE,则OE⊥平面ABC,
解:设△ABC的中心为E,AB中点为D,连结OE,则OE⊥平面ABC,
∴OE⊥CE.
∵O是PC的中点,∴P到平面ABC的距离h=2OE.
由正三角形的性质可得CD=$\sqrt{3}$,CE=$\frac{2}{3}CD$=$\frac{2\sqrt{3}}{3}$.
∴OE=$\sqrt{O{C}^{2}-C{E}^{2}}$=$\sqrt{4-\frac{4}{3}}$=$\frac{2\sqrt{6}}{3}$.
∴h=$\frac{4\sqrt{6}}{3}$.
∴三棱锥的体积V=$\frac{1}{3}{S}_{△ABC}•h$=$\frac{1}{3}×\frac{\sqrt{3}}{4}×{2}^{2}×\frac{4\sqrt{6}}{3}$=$\frac{4\sqrt{2}}{3}$.
故选B.
点评 本题考查了棱锥与外接球的关系,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
14.若点P在抛物线y=x2上,点Q(0,3),则|PQ|的最小值是( )
| A. | $\frac{\sqrt{13}}{2}$ | B. | $\frac{\sqrt{11}}{2}$ | C. | 3 | D. | $\sqrt{5}$ |
15.设函数f(x)=2sin(ωx-$\frac{π}{3}$),已知f(α)=-2,f(β)=0,且|α-β|的最小值是$\frac{π}{4}$,现将y=f(x)的图象向左平移φ(φ>0)个单位,所得函数图象关于y轴对称,则φ的最小值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{12}$ | D. | $\frac{5π}{12}$ |
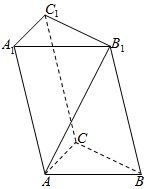 如图,在三棱柱ABC-A1B1C1中,AB=AC,且侧面BB1C1C是菱形,∠B1BC=60°.
如图,在三棱柱ABC-A1B1C1中,AB=AC,且侧面BB1C1C是菱形,∠B1BC=60°.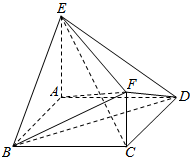 如图,已知多面体A-BCDEF中,ABCD为菱形,∠ABC=60°,AE⊥平面ABCD,AE∥CF,AB=AE=1,AF⊥BE.
如图,已知多面体A-BCDEF中,ABCD为菱形,∠ABC=60°,AE⊥平面ABCD,AE∥CF,AB=AE=1,AF⊥BE.