题目内容
8.已知双曲线的一条渐近线方程是y=$\sqrt{3}$x,它的一个焦点在抛物线y2=8x的准线上,则该双曲线的标准方程为x2-$\frac{{y}^{2}}{3}$=1.分析 求出抛物线的准线方程,可得c=2,设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0),求出渐近线方程,由题意可得a,b的方程,解方程可得a,b,进而得到双曲线的方程.
解答 解:抛物线y2=8x的准线为x=-2,
由题意可得c=2,
设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0),
渐近线方程为y=±$\frac{b}{a}$x,
由题意可得a2+b2=4,b=$\sqrt{3}$a,
解得a=1,b=$\sqrt{3}$,
即有双曲线的标准方程为x2-$\frac{{y}^{2}}{3}$=1.
故答案为:x2-$\frac{{y}^{2}}{3}$=1.
点评 本题考查双曲线的方程的求法,注意运用抛物线的准线方程和渐近线方程,考查运算能力,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
1.若数列{an}满足a1=1,a2=$\frac{2}{3}$,2an-1an+1=anan+1+an-1an(n≥2),则an=( )
| A. | $\frac{2}{n+1}$ | B. | $\frac{2}{n+2}$ | C. | ($\frac{2}{3}$)n | D. | ($\frac{2}{3}$)n-1 |
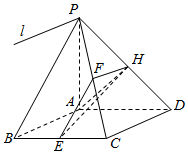 如图,已知四棱锥P-ABCD的底面是菱形,PA⊥平面ABCD,∠ABC=60°,E,F,H分别是BC,PC,PD的中点.
如图,已知四棱锥P-ABCD的底面是菱形,PA⊥平面ABCD,∠ABC=60°,E,F,H分别是BC,PC,PD的中点.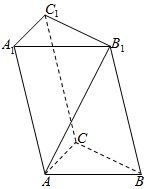 如图,在三棱柱ABC-A1B1C1中,AB=AC,且侧面BB1C1C是菱形,∠B1BC=60°.
如图,在三棱柱ABC-A1B1C1中,AB=AC,且侧面BB1C1C是菱形,∠B1BC=60°.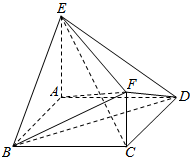 如图,已知多面体A-BCDEF中,ABCD为菱形,∠ABC=60°,AE⊥平面ABCD,AE∥CF,AB=AE=1,AF⊥BE.
如图,已知多面体A-BCDEF中,ABCD为菱形,∠ABC=60°,AE⊥平面ABCD,AE∥CF,AB=AE=1,AF⊥BE.