题目内容
11.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线的倾斜角为$\frac{2π}{3}$,离心率为e,$\frac{{a}^{2}+{e}^{2}}{b}$最小值为$\frac{4\sqrt{3}}{3}$.分析 求出双曲线的渐近线方程,由题意可得b=$\sqrt{3}$a,c=2a,e=$\frac{c}{a}$=2,再由基本不等式可得最小值.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的渐近线方程为y=±$\frac{b}{a}$x,
由题意可得-$\frac{b}{a}$=tan$\frac{2π}{3}$=-$\sqrt{3}$,
即有b=$\sqrt{3}$a,c=2a,e=$\frac{c}{a}$=2,
则$\frac{{a}^{2}+{e}^{2}}{b}$=$\frac{{a}^{2}+4}{\sqrt{3}a}$
=$\frac{\sqrt{3}}{3}$(a+$\frac{4}{a}$)≥$\frac{\sqrt{3}}{3}$•2$\sqrt{a•\frac{4}{a}}$=$\frac{4\sqrt{3}}{3}$.
当且仅当a=2时,取得最小值$\frac{4\sqrt{3}}{3}$.
故答案为:$\frac{{4\sqrt{3}}}{3}$.
点评 本题考查双曲线的方程和性质,考查离心率公式的运用,以及基本不等式的运用:求最值,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知F是双曲线$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1的右焦点,点P的坐标为(3,1),点A在双曲线上,则|AP|+|AF|的最小值为( )
| A. | $\sqrt{37}$+4 | B. | $\sqrt{37}$-4 | C. | $\sqrt{37}$-2$\sqrt{5}$ | D. | $\sqrt{37}$+2$\sqrt{5}$ |
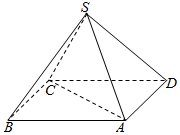 如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充.已知金字塔的每一条棱和边都相等
如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充.已知金字塔的每一条棱和边都相等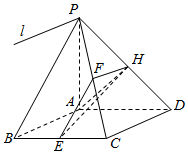 如图,已知四棱锥P-ABCD的底面是菱形,PA⊥平面ABCD,∠ABC=60°,E,F,H分别是BC,PC,PD的中点.
如图,已知四棱锥P-ABCD的底面是菱形,PA⊥平面ABCD,∠ABC=60°,E,F,H分别是BC,PC,PD的中点.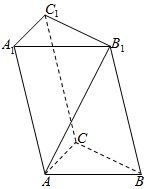 如图,在三棱柱ABC-A1B1C1中,AB=AC,且侧面BB1C1C是菱形,∠B1BC=60°.
如图,在三棱柱ABC-A1B1C1中,AB=AC,且侧面BB1C1C是菱形,∠B1BC=60°.