题目内容
13．函数f（x）=$\sqrt{\frac{1}{lgx}-2}$的定义域为（1，$\sqrt{10}$]．分析 要使函数有意义，则$\left\{\begin{array}{l}{\frac{1}{lgx}-2≥0}\\{x＞0且x≠1}\end{array}\right.$，解得即可．
解答 解：要使函数有意义，则$\left\{\begin{array}{l}{\frac{1}{lgx}-2≥0}\\{x＞0且x≠1}\end{array}\right.$，
由$\frac{1}{lgx}$-2≥0转化为（1-2lgx）lgx≥0，且x≠1即（lgx-$\frac{1}{2}$）lgx≤0，且x≠1
解得0＜lgx≤$\frac{1}{2}$，即lg1＜lgx≤lg$\sqrt{10}$，
解得1＜x≤$\sqrt{10}$
故函数的定义域为（1，$\sqrt{10}$]，
故答案为：（1，$\sqrt{10}$]．
点评 本题考查了函数定义域的求法，关键是解不等式组，属于基础题．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
1．若数列{an}满足a1=1，a2=$\frac{2}{3}$，2an-1an+1=anan+1+an-1an（n≥2），则an=（ ）
| A． | $\frac{2}{n+1}$ | B． | $\frac{2}{n+2}$ | C． | （$\frac{2}{3}$）n | D． | （$\frac{2}{3}$）n-1 |
8．若函数f（x）=sin（ωx+φ）+$\sqrt{3}$cos（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）为偶函数，且在区间（$\frac{3π}{4}$，π）上单调递增，则ω的最小值为（ ）
| A． | 2 | B． | $\frac{4}{3}$ | C． | 1 | D． | $\frac{3}{4}$ |
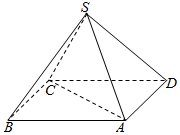如图，某人打算做一个正四棱锥形的金字塔模型，先用木料搭边框，再用其他材料填充．已知金字塔的每一条棱和边都相等
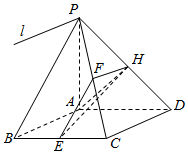如图，已知四棱锥P-ABCD的底面是菱形，PA⊥平面ABCD，∠ABC=60°，E，F，H分别是BC，PC，PD的中点．