题目内容
20.计算下列各式:①log2$\frac{1}{8}$ ②$(\frac{16}{9})^{-\frac{3}{2}}$ ③sin600° ④cos(-1020°)
分析 ①利用对数的运算性质和运算法则求解.
②利用指数的运算性质和运算法则求解.
③把原式的角度600°变形为2×360°-120°,然后利用诱导公式化简,再把120°变为180°-60°,利用诱导公式及特殊角的三角函数值即可求出值.
④首先利用诱导公式将cos(-1020°)转化成cos60°,再利用特殊角函数值求出结果.
解答 解:①log2$\frac{1}{8}$=0-3=-3.
②$(\frac{16}{9})^{-\frac{3}{2}}$=($\frac{4}{3}$)${\;}^{2×(-\frac{3}{2})}$=$\frac{27}{64}$.
③sin600°=sin(2×360°-120°)=-sin120°=-sin(180°-60°)=-sin60°=-$\frac{\sqrt{3}}{2}$.
④cos(-1020°)=cos1020°=cos(3×2π°-60°)=cos60°=$\frac{1}{2}$.
点评 此题主要考查了对数及指数的运算性质和运算法则,运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键,同时注意角度的灵活变换.

练习册系列答案
相关题目
10.已知圆C:x2+y2-2x-1=0,直线l:3x-4y+12=0,圆C上任意一点P到直线l的距离小于2的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
8.若f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x}-a.x≥\frac{1}{2}}\\{x+2-a,x<\frac{1}{2}}\end{array}\right.$的三个零点为x1,x2,x3,则x1x2x3的取值范围是( )
| A. | (0,+∞) | B. | (0,$\frac{3}{2}$) | C. | (0,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,$\frac{3}{2}$) |
5.已知sin(π+a)=$\frac{1}{2}$,则sin(9π+a)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
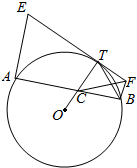 已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证:
已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证: