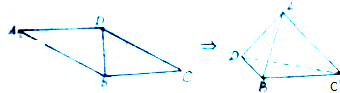
题目内容
已知ABCD中,AD=BC.AD∥BC,且AB=3
,AD=2
.BD=
,沿BD将其折成一个二面角A-BD-C,使得AB⊥CD.
(1)求二面角A-BD-C的大小;
(2)求折后点A到面BCD的距离.
| 2 |
| 3 |
| 6 |
(1)求二面角A-BD-C的大小;
(2)求折后点A到面BCD的距离.

考点:与二面角有关的立体几何综合题,点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:(1)作AO⊥平面BCD于O,连接BO,则∠ABO为AB与平面BCD所成角.由AB⊥CD,BO是AB在平面BCD上的射影,知CD⊥BO.由AD⊥BD,可得∠ADO为二面角A-BD-C的平面角,求出cos∠ABO=
,可得AO,即可得出结论;
(2)由(1)知,AO=3,即折后点A到面BCD的距离.
| ||
| 2 |
(2)由(1)知,AO=3,即折后点A到面BCD的距离.
解答:
 解:(1)作AO⊥平面BCD于O,连接BO,
解:(1)作AO⊥平面BCD于O,连接BO,
则∠ABO为AB与平面BCD所成角.
∵AB⊥CD,BO是AB在平面BCD上的射影,
∴CD⊥BO
∵AB=3
,AD=2
,BD=
,
∴AD⊥BD,
∴∠ADO为二面角A-BD-C的平面角.
∵cos∠ABD=cos∠DBO•cos∠ABO,
∴
=
•cos∠ABO,
∴cos∠ABO=
∴AO=3,
∴sin∠ADO=
=
,
∴∠ADO=60°;
(2)由(1)知,AO=3,即折后点A到面BCD的距离为3.
 解:(1)作AO⊥平面BCD于O,连接BO,
解:(1)作AO⊥平面BCD于O,连接BO,则∠ABO为AB与平面BCD所成角.
∵AB⊥CD,BO是AB在平面BCD上的射影,
∴CD⊥BO
∵AB=3
| 2 |
| 3 |
| 6 |
∴AD⊥BD,
∴∠ADO为二面角A-BD-C的平面角.
∵cos∠ABD=cos∠DBO•cos∠ABO,
∴
| ||
3
|
2
| ||
3
|
∴cos∠ABO=
| ||
| 2 |
∴AO=3,
∴sin∠ADO=
| 3 | ||
2
|
| ||
| 2 |
∴∠ADO=60°;
(2)由(1)知,AO=3,即折后点A到面BCD的距离为3.
点评:本题考查折后二面角A-BD-C的大小,折后点A到面BCD的距离.考查化归与转化思想.综合性强,难度大,确定折后点A到面BCD的距离是关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
若A、B为锐角△ABC的两个锐角,函数f(x)在(0,1)上是单减函数,则( )
| A、f(sinA)>f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(cosA)=f(sinB) |
| D、f(cosA)>f(sinB) |
函数y=1-sinx,x∈[0,2π]的图象与直线y=
交点的个数是( )
| 3 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
已知正方形ABCD的边长为2,P是平面ABCD外一点,且PA=PB=PC=PD=2
,则PA与平面ABCD所成的角是( )
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|