题目内容
函数y=1-sinx，x∈[0，2π]的图象与直线y=
交点的个数是（ ）
| 3 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
考点：正弦函数的图象
专题：三角函数的求值
分析：根据曲线与方程之间的关系，直接解方程即可得到结论．
解答：
解：由y=1-sinx=
，得sinx=-
，
∴当x∈[0，2π]时，x=
或x=
，
即方程有2个解，即两条曲线的图象的交点个数为2个．
故选：C．
| 3 |
| 2 |
| 1 |
| 2 |
∴当x∈[0，2π]时，x=
| 7π |
| 6 |
| 11π |
| 6 |
即方程有2个解，即两条曲线的图象的交点个数为2个．
故选：C．
点评：本题主要考查函数交点个数的判断，利用函数和方程之间的关系，直接进行求解即可，比较基础．
练习册系列答案
同步练习强化拓展系列答案
相关题目
已知函数f（x）=（x+α）cosx为奇函数，则a= ；现将函数f（x）的图象沿x轴向左平移
个单位，得到的图象所对应的函数记为g（x），那么其解析式g（x）= ；且函数g（x）图象的对称中心为 ．
| π |
| 2 |
已知f（x）=
sinxcosx-cos2x+
，在△ABC中，角A，B，C的对边分别是a，b，c，且满足2bcosA≤2c-
a，则f（B）的取值范围（ ）
| 3 |
| 1 |
| 2 |
| 3 |
A、（-1，
| ||||||||
B、（-
| ||||||||
C、（-
| ||||||||
D、（-
|
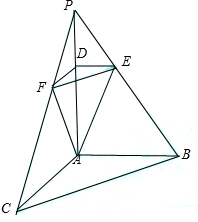在三棱椎P-ABC中，PA⊥平面ABC，AC=AB=