题目内容
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
(Ⅰ)求n的值;
(Ⅱ)把在前排就坐的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖,求a和b至少有一人上台抽奖的概率.
(Ⅰ)求n的值;
(Ⅱ)把在前排就坐的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖,求a和b至少有一人上台抽奖的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)根据分层抽样可得
=
,故可求n的值;
(Ⅱ)求出高二代表队6人,从中抽取2人上台抽奖的基本事件,确定a和b至少有一人上台抽奖的基本事件,根据古典概型的概率公式,可得a和b至少有一人上台抽奖的概率;
| 6 |
| 120 |
| 20 |
| 120+120+n |
(Ⅱ)求出高二代表队6人,从中抽取2人上台抽奖的基本事件,确定a和b至少有一人上台抽奖的基本事件,根据古典概型的概率公式,可得a和b至少有一人上台抽奖的概率;
解答:
解:(Ⅰ)依题意,
=
,…(2分)
解得n=160; …(4分)
(Ⅱ)记事件A为“a和b至少有一人上台抽奖”,
从高二代表队6人中抽取2人上台抽奖的所有基本事件列举如下:
(a,b),(a,c),(a,d),(a,e),(a,f),
(b,c),(b,d),(b,e),(b.f),(c,d),
(c,e),(c,f),(d,e),(d,f),(e,f) …(7分)
共15种可能,…(8分)
其中事件A包含的基本事件有9种,即:
(a,b),(a,c),(a,d),(a,e),(a,f),
(b,c),(b,d),(b,e),(b.f),…(10分)
所以P(A)=
=
…(12分)
| 6 |
| 120 |
| 20 |
| 120+120+n |
解得n=160; …(4分)
(Ⅱ)记事件A为“a和b至少有一人上台抽奖”,
从高二代表队6人中抽取2人上台抽奖的所有基本事件列举如下:
(a,b),(a,c),(a,d),(a,e),(a,f),
(b,c),(b,d),(b,e),(b.f),(c,d),
(c,e),(c,f),(d,e),(d,f),(e,f) …(7分)
共15种可能,…(8分)
其中事件A包含的基本事件有9种,即:
(a,b),(a,c),(a,d),(a,e),(a,f),
(b,c),(b,d),(b,e),(b.f),…(10分)
所以P(A)=
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题考查古典概型的计算,涉及列举法的应用,注意结合题意中“写出所有可能的结果”的要求,使用列举法,注意按一定的顺序列举,做到不重不漏.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
在△ABC中,a=2
,A=30°,B=120°,则b等于( )
| 3 |
| A、4 | ||
B、2
| ||
| C、6 | ||
D、6
|
| a |
| COSA |
| b |
| COSB |
| c |
| COSC |
| A、等腰直角三角形 |
| B、等边三角形 |
| C、顶角为120°的等腰三角形 |
| D、以上均不正确 |
方程x3=3x-1的三根x1,x2,x3,其中x1<x2<x3,则x2所在的区间为( )
| A、(-2,-1) | ||
| B、(0,1) | ||
C、(1,
| ||
D、(
|
 已知椭圆C:
已知椭圆C: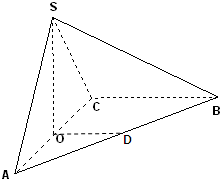 在三棱锥S-ABC中,平面SAC⊥平面ABC,且△SAC是正三角形,O是AC的中点,D是AB的中点.
在三棱锥S-ABC中,平面SAC⊥平面ABC,且△SAC是正三角形,O是AC的中点,D是AB的中点.