题目内容
 已知抛物线y2=2px(p>0)上的任意一点P到该抛物线焦点的距离比该点到y轴的距离多1.
已知抛物线y2=2px(p>0)上的任意一点P到该抛物线焦点的距离比该点到y轴的距离多1. (Ⅰ)求p的值;
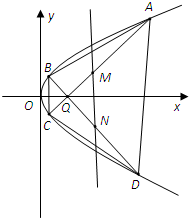
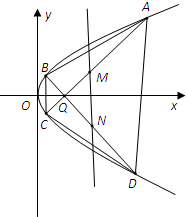
(Ⅱ)如图所示,过定点Q(2,0)且互相垂直的两条直线l1、l2分别与该抛物线分别交于A、C、B、D四点.
(i)求四边形ABCD面积的最小值;
(ii)设线段AC、BD的中点分别为M、N两点,试问:直线MN是否过定点?若是,求出定点坐标;若不是,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线中的最值与范围问题
分析:(Ⅰ)由题意可知
=1;
(Ⅱ)(i)由题意可设直线?1的方程为x=2+my(m≠0),代入y2=4x得y2-4my-8=0,由韦达定理及弦长公式可表示出|AC|、|BD|,从而可表示出S四边形ABCD=
|AC||BD|,通过换元及二次函数的性质可求得最小值;(ii)由(i)及中点坐标公式可得M、N的坐标,从而可表示直线MN的方程,根据方程特点可求得定点坐标;
| p |
| 2 |
(Ⅱ)(i)由题意可设直线?1的方程为x=2+my(m≠0),代入y2=4x得y2-4my-8=0,由韦达定理及弦长公式可表示出|AC|、|BD|,从而可表示出S四边形ABCD=
| 1 |
| 2 |
解答:
 解:(Ⅰ)由已知
解:(Ⅰ)由已知
=1,∴p=2;
(Ⅱ)(i)由题意可设直线?1的方程为x=2+my(m≠0),代入y2=4x得y2-4my-8=0,
设A(x1,y1),C(x2,y2),则
,△=16(2+m2)>0,
∴|AC|=
=
=4
=4
,
同理可得|BD|=4
,
∴S四边形ABCD=
|AC|•|BD|=8
=8
=8
,
设t=m2+
,则t≥2,
∴S四边形ABCD=8
,
∵函数y=2t2+9t+10在[2,+∞)上是增函数,
∴S四边形ABCD ≥8
=48,当且仅当t=2即m=±1时取等号,
∴四边形ABCD面积的最小值是48.
(ii)由(i)得y1+y2=4m,
∴yM=
=2m,xM=2+myM=2+2m2,
∴M(2+2m2,2m),
同理得N(2+
,-
),
∴直线的方程可表示为(y-2m)(
-2m2)=(-
-2m)(x-2-2m2),即(y-2m)(1-m2)=-m(x-2-2m2),
当y=0时得x=4,
∴直线MN过定点(4,0).
 解:(Ⅰ)由已知
解:(Ⅰ)由已知| p |
| 2 |
(Ⅱ)(i)由题意可设直线?1的方程为x=2+my(m≠0),代入y2=4x得y2-4my-8=0,
设A(x1,y1),C(x2,y2),则
|
∴|AC|=
| (m2+1)[(y1-y2)2-4y1y2] |
=
| (m2+1)(16m2+32) |
| (m2+1)(m2+2) |
| m4+3m2+2 |
同理可得|BD|=4
|
∴S四边形ABCD=
| 1 |
| 2 |
(m4+3m2+2)(
|
=8
2(m4+
|
2(m2+
|
设t=m2+
| 1 |
| m2 |
∴S四边形ABCD=8
| 2t2+9t+10 |
∵函数y=2t2+9t+10在[2,+∞)上是增函数,
∴S四边形ABCD ≥8
| 36 |
∴四边形ABCD面积的最小值是48.
(ii)由(i)得y1+y2=4m,
∴yM=
| y1+y2 |
| 2 |
∴M(2+2m2,2m),
同理得N(2+
| 2 |
| m2 |
| 2 |
| m |
∴直线的方程可表示为(y-2m)(
| 2 |
| m2 |
| 2 |
| m |
当y=0时得x=4,
∴直线MN过定点(4,0).
点评:本题考查抛物线的性质、方程,考查直线与抛物线的位置关系、四边形的面积求解,运算量较大,综合性较强.第(Ⅱ)中的第(i)问:
S四边形ABCD=
|AC|•|BD|=8
•
=8
=8
≥8
=48(当且仅当m=±1时取等号)也可.
S四边形ABCD=
| 1 |
| 2 |
| (m2+1)(m2+2) |
(
|
[(m2+1)(
|
(2+m2+
|
| (2+2)(5+2×2) |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程x3=3x-1的三根x1,x2,x3,其中x1<x2<x3,则x2所在的区间为( )
| A、(-2,-1) | ||
| B、(0,1) | ||
C、(1,
| ||
D、(
|
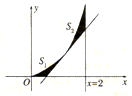 已知l1为函数f(x)=x2(x∈[0,2])在P(t,t2)(t∈(0,2))处的切线,l2为x=2,f(x),l1,l2与x轴所围成的图形如图所示.
已知l1为函数f(x)=x2(x∈[0,2])在P(t,t2)(t∈(0,2))处的切线,l2为x=2,f(x),l1,l2与x轴所围成的图形如图所示.