题目内容
设数列{an}的前n项和为Sn,且对任意n∈N*都有:(Sn-1)2=anSn;
(1)求S1,S2,S3;
(2)猜想Sn的表达式并证明.
(1)求S1,S2,S3;
(2)猜想Sn的表达式并证明.
考点:数学归纳法,归纳推理
专题:综合题,点列、递归数列与数学归纳法
分析:(1)由(Sn-1)2=anSn,可得Sn=
,即可求S1,S2,S3;
(2)猜想Sn=
,再用数学归纳法证明.
| 1 |
| 2-Sn-1 |
(2)猜想Sn=
| n |
| n+1 |
解答:
解:(1)∵(Sn-1)2=anSn,
∴(Sn-1)2=(Sn-Sn-1)Sn,
∴Sn=
,
又(S1-1)2=S12,
∴S1=
,S2=
,S3=
,
(2)猜想Sn=
.下面用数学归纳法证明:
1°当n=1时,S1=
,
=
,猜想正确;
2°假设当n=k时,猜想正确,即Sk=
,
那么,n=k+1时,由Sk+1=
=
=
,猜想也成立,
综上知,Sn=
对一切自然数n均成立.
∴(Sn-1)2=(Sn-Sn-1)Sn,
∴Sn=
| 1 |
| 2-Sn-1 |
又(S1-1)2=S12,
∴S1=
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
(2)猜想Sn=
| n |
| n+1 |
1°当n=1时,S1=
| 1 |
| 2 |
| n |
| n+1 |
| 1 |
| 2 |
2°假设当n=k时,猜想正确,即Sk=
| k |
| k+1 |
那么,n=k+1时,由Sk+1=
| 1 |
| 2-Sk |
| 1 | ||
2-
|
| k+1 |
| (k+1)+1 |
综上知,Sn=
| n |
| n+1 |
点评:数学归纳法的关键是递推环节,要符合假设的模型才能成立.

练习册系列答案
相关题目
关于直线a,b,l以及平面M,N,下面命题中正确的是( )
| A、若a∥M,b∥M,则a∥b |
| B、若a∥M,b⊥a,则b⊥M |
| C、若a⊥M,a∥N,则M⊥N |
| D、若a?M,b?M,且l⊥a,l⊥b,则l⊥M |
方程x3=3x-1的三根x1,x2,x3,其中x1<x2<x3,则x2所在的区间为( )
| A、(-2,-1) | ||
| B、(0,1) | ||
C、(1,
| ||
D、(
|
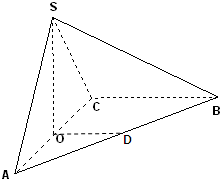 在三棱锥S-ABC中,平面SAC⊥平面ABC,且△SAC是正三角形,O是AC的中点,D是AB的中点.
在三棱锥S-ABC中,平面SAC⊥平面ABC,且△SAC是正三角形,O是AC的中点,D是AB的中点.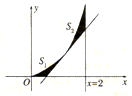 已知l1为函数f(x)=x2(x∈[0,2])在P(t,t2)(t∈(0,2))处的切线,l2为x=2,f(x),l1,l2与x轴所围成的图形如图所示.
已知l1为函数f(x)=x2(x∈[0,2])在P(t,t2)(t∈(0,2))处的切线,l2为x=2,f(x),l1,l2与x轴所围成的图形如图所示.