题目内容
7.已知函数$f(x)=\left\{\begin{array}{l}{x^2}-1{,_{\;}}x≤0\\ x-1{,_{\;}}x>0\end{array}\right.$,g(x)=2x-1,则f(g(2))=2,f[g(x)]的值域为[-1,+∞).分析 由题意先求出g(2),代入f(x)的解析式求得f(g(2));求出g(x)的值域,再结合分段函数求得f(g(x))在不同区间上的值域,取并集得答案.
解答 解:∵$f(x)=\left\{\begin{array}{l}{x^2}-1{,_{\;}}x≤0\\ x-1{,_{\;}}x>0\end{array}\right.$,g(x)=2x-1,
∴g(2)=3,则f(g(2))=f(3)=2;
∵g(x)=2x-1>-1,
∴当g(x)∈(-1,0]时,f(g(x))∈[-1,0);
当g(x)∈(0,+∞)时,f(g(x))∈(-1,+∞).
取并集得f(g(x))∈[-1,+∞).
故答案为:2,[-1,+∞).
点评 本题考查分段函数值域的求法,考查运算能力,是中档题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
17.下列事件中:①任取三条线段,这三条线段恰好组成直角三角形;②从一个三角形的三个顶点各任画一条射线,这三条射线交于一点;③实数a,b都不为0,但a2+b2=0;④明年12月28日的最高气温高于今年12月10日的最高气温,其中为随机事件的是( )
| A. | ①②③④ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
18.已知函数f(x)=sin(ωx-$\frac{π}{12}$)+cos(ωx-$\frac{π}{12}$)(0<ω<10)的图象关于直线x=1对称,则满足条件的ω的值的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.设x,y满足约束条件$\left\{\begin{array}{l}{x≤3}\\{x-y+5≥0}\\{x+y≥0}\end{array}\right.$,若$\overline{a}$=(y,1),$\overline{b}$=($\frac{1}{x+1}$,0),则z=$\overline{a}•\overline{b}$的取值范围是( )
| A. | [-$\frac{5}{3}$,-$\frac{3}{4}$] | B. | (-∞,-$\frac{5}{3}$] | C. | (-∞,-$\frac{5}{3}$]∩[-$\frac{3}{4}$,+∞) | D. | [-$\frac{3}{4}$,+∞) |
16.现要完成下列3项抽样调查:
①从10盒黑色水笔芯中抽取2盒进行质量检查.
②天空影院有32排,每排有60个座位,《速度与激情7》首映当晚,恰好坐满了观众,电影结束后,为了听取意见,需要请32名观众进行座谈.
③抚州市某中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名.为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.
请问较为合理的抽样方法是( )
①从10盒黑色水笔芯中抽取2盒进行质量检查.
②天空影院有32排,每排有60个座位,《速度与激情7》首映当晚,恰好坐满了观众,电影结束后,为了听取意见,需要请32名观众进行座谈.
③抚州市某中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名.为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.
请问较为合理的抽样方法是( )
| A. | ①系统抽样,②简单随机抽样,③分层抽样 | |
| B. | ①简单随机抽样,②分层抽样,③系统抽样 | |
| C. | ①简单随机抽样,②系统抽样,③分层抽样 | |
| D. | ①分层抽样,②系统抽样,③简单随机抽样 |
17.设f(x)=$\left\{\begin{array}{l}{x,x>0}\\{1-x,x<0}\end{array}\right.$,则有( )
| A. | f(f(x))=(f(x))2 | B. | f(f(x))=f(x) | C. | f(f(x))>f(x) | D. | f(f(x))<f(x) |
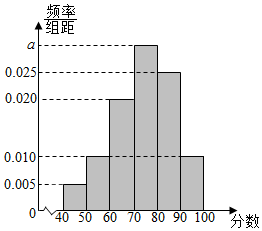 某校从高二年级学生中随机抽取40名学生,将他们的期中考试政治成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),[60,70),[70,80)[80,90),[90,100]后,得到如图所示的频率分布直方图.
某校从高二年级学生中随机抽取40名学生,将他们的期中考试政治成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),[60,70),[70,80)[80,90),[90,100]后,得到如图所示的频率分布直方图.