题目内容

19．已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=log2（x+1），则函数f（x）的大致图象是（　　）
A．B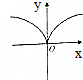．C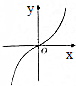．D．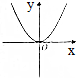

分析 由题意可得函数f（x）的图象关于原点对称，函数在R上单调递增，且增长比较缓慢，从而结合选项得出结论

解答 解：由函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=log2（x+1），
可得函数f（x）的图象关于原点对称，函数在R上单调递增，且增长比较缓慢，
结合所给的选项，
故选：A．

点评 本题主要考查函数的奇偶性、单调性的应用，函数的图象特征，属于中档题．

练习册系列答案
相关题目
9．已知函数f（x）=x2+2xsinθ-1，x∈[-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$]．
（Ⅰ）当sinθ=-$\frac{1}{2}$，求f（x）的最大值和最小值；
（Ⅱ）若f（x）在x∈[-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$]上是单调函数，且θ∈[0，2π]，求θ的取值范围．
10．在△ABC中，三内角A，B，C的对边分别为a，b，c，
命题p：若a＞acosB+bcosA，则A＞C；
命题q：若A＞B，则sinA＞sinB，
给出下列四个结论：
①命题q的逆命题、否命题、逆否命题是真命题；
②命题“p∧q”是假命题；
③命题“p∨￢q”是假命题；
④命题“￢p∨￢q”是假命题，
其中所有正确结论法的序号是①④．
7．已知函数$f（x）=\left\{\begin{array}{l}{x^2}-1{，_{\;}}x≤0\\ x-1{，_{\;}}x＞0\end{array}\right.$，g（x）=2x-1，则f（g（2））=2，f[g（x）]的值域为[-1，+∞）．
14．设a=（$\frac{2}{3}$）${\;}^{\frac{1}{3}}$，b=（$\frac{1}{3}$）${\;}^{\frac{2}{3}}$，c=（$\frac{2}{3}$）${\;}^{\frac{2}{3}}$，则a，b，c大小关系是（　　）
A．a＞b＞cB．a＞c＞bC．c＞a＞bD．b＞c＞a
4．已知sinα=-$\frac{\sqrt{10}}{10}$，且α∈（π，$\frac{3π}{2}$），则tan2α=（　　）
A．$\frac{3}{4}$B．-$\frac{3}{4}$C．$\frac{1}{3}$D．-$\frac{1}{3}$
11．设函数f（x）=2sinxcos2$\frac{φ}{2}$+cosxsinφ-sinx（0＜φ＜π）在x=π处取最小值．
（I）求ϕ的值，并化简f（x）；
（Ⅱ）在△ABC中，a，b，c分别是角A，B，C的对边，已知a=1，b=$\sqrt{2}$，f（A）=$\frac{{\sqrt{3}}}{2}$，求角C．
8．函数y=sin（x+$\frac{2}{3}$π）在[0，2π]上的单调递增区间是[$\frac{5π}{6}$，$\frac{11π}{6}$]．
9．求下列函数的定义域
（1）y=log2（5+4x-x2）+$\frac{1}{{2}^{x}-8}$；
（2）y=$\frac{1}{\sqrt{1{-0.5}^{x}}}$+lg（2-x）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网