△ABC的内角A.B.C的对边分别为a.b.c．已知$a=\sqrt{3}.b=2$.A=60°.则c=( )A．$\frac{1}{2}$B．1C．$\sqrt{3}$D．2 题目和参考答案——青夏教育精英家教网—

题目内容

5．△ABC的内角A，B，C的对边分别为a，b，c．已知$a=\sqrt{3}，b=2$，A=60°，则c=（　　）

A．

$\frac{1}{2}$

B．

C．

$\sqrt{3}$

D．

分析由已知利用余弦定理即可计算得解．

解答解：∵$a=\sqrt{3}，b=2$，A=60°，
∴由余弦定理a²=b²+c²-2bccosA，可得：3=4+c²-2×$2×c×\frac{1}{2}$，整理可得：c²-2c+1=0，
∴解得：c=1．
故选：B．

点评本题主要考查了余弦定理在解三角形中的应用，考查了转化思想，属于基础题．

练习册系列答案

16．

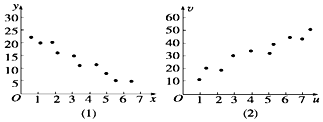对变量x，y有观测数据（x_i，y_i）（i=1，2，…，10），得散点图（1）；对变量u，v，有观测数据（u_i，v_i）（i=1，2，…，10），得散点图（2），由这两个散点图可以判断（　　）

	A．	变量x与y正相关，u与v正相关		B．	变量x与y正相关，u与v负相关
	C．	变量x与y负相关，u与v正相关		D．	变量x与y负相关，u与v负相关

13．命题：“?x∈R，x²-ax+1＜0”的否定为?x∈R，x²-ax+1≥0．

20．已知函数$f（x）={e^x}-\frac{1}{2}a{x^2}$（x＞0，e为自然对数的底数），f'（x）是f（x）的导函数．
（Ⅰ）当a=2时，求证f（x）＞1；
（Ⅱ）是否存在正整数a，使得f'（x）≥x²lnx对一切x＞0恒成立？若存在，求出a的最大值；若不存在，说明理由．

10．已知函数f（x）是定义在实数集R上的奇函数，若x＞0时，f（x）=x•e^x，则不等式f（x）＞3x的解集为（　　）

	A．	{x\|-ln3＜x＜ln3}		B．	{x\|x＜-ln3，或x＞ln3}
	C．	{x\|-ln3＜x＜0，或x＞ln3}		D．	{x\|x＜-ln3，或0＜x＜ln3}

17．已知数列{a_n}的前n项和为S_n．，且${S_n}={n^2}-2n$．
（Ⅰ）求{a_n}通项公式；
（Ⅱ）设${b_n}=n•{2^{{a_n}+1}}$，求数列{b_n}前n项的和T_n．

14．设i是虚数单位，复数i（1+ai）为纯虚数，则实数a为（　　）

15．已知直线l：y=k（x+$\sqrt{3}$）和圆C：x²+（y-1）²=1，若直线l与圆C相切，则k=（　　）

$\frac{\sqrt{3}}{3}$或0

D．

$\sqrt{3}$或0

试题分类