题目内容
16．
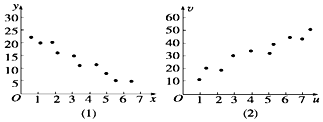对变量x，y有观测数据（xi，yi）（i=1，2，…，10），得散点图（1）；对变量u，v，有观测数据（ui，vi）（i=1，2，…，10），得散点图（2），由这两个散点图可以判断（ ）| A． | 变量x与y正相关，u与v正相关 | B． | 变量x与y正相关，u与v负相关 | ||
| C． | 变量x与y负相关，u与v正相关 | D． | 变量x与y负相关，u与v负相关 |
分析 通过观察散点图得出：y随x的增大而减小，各点整体呈下降趋势，x与y负相关，
u随v的增大而增大，各点整体呈上升趋势，u与v正相关．
解答 解：由题图1可知，y随x的增大而减小，各点整体呈下降趋势，x与y负相关，
由题图2可知，u随v的增大而增大，各点整体呈上升趋势，u与v正相关．
故选：C．
点评 本题考查了散点图的应用问题，通过读图来解决问题，是基础题．
练习册系列答案
相关题目
如图，在四面体ABCD中，已知∠ABD=∠CBD=60°，AB=BC=2，CE⊥BD于E
4．若集合A={x∈R|x2-3x≤0}，B={1，2}，则A∩B=（ ）
| A． | {x|0≤x≤3} | B． | {1，2} | C． | {0，1，2} | D． | {0，1，2，3} |
11．已知焦点在y轴上的双曲线C的中心是原点O，离心率等于$\frac{{\sqrt{5}}}{2}$，以双曲线C的一个焦点为圆心，2为半径的圆与双曲线C的渐近线相切，则双曲线C的方程为（ ）
| A． | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B． | $\frac{y^2}{4}-{x^2}=1$ | C． | ${y^2}-\frac{x^2}{4}=1$ | D． | $\frac{y^2}{16}-\frac{x^2}{4}=1$ |
1．双曲线$\frac{x^2}{m}-\frac{y^2}{n}=1（{m＞0，n＞0}）$和椭圆$\frac{x^2}{a}+\frac{y^2}{b}=1（{a＞b＞0}）$有相同的焦点F1，F2，M为两曲线的交点，则|MF1|•|MF2|等于（ ）
| A． | a+m | B． | b+m | C． | a-m | D． | b-m |
8．△ABC的内角A，B，C的对边分别为a，b，c，若$cosC=\frac{{2\sqrt{2}}}{3}$，bcosA+acosB=2，则△ABC的外接圆的面积为（ ）
| A． | 4π | B． | 8π | C． | 9π | D． | 36π |
5．△ABC的内角A，B，C的对边分别为a，b，c．已知$a=\sqrt{3}，b=2$，A=60°，则c=（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $\sqrt{3}$ | D． | 2 |