题目内容
20.已知函数$f(x)={e^x}-\frac{1}{2}a{x^2}$(x>0,e为自然对数的底数),f'(x)是f(x)的导函数.(Ⅰ)当a=2时,求证f(x)>1;
(Ⅱ)是否存在正整数a,使得f'(x)≥x2lnx对一切x>0恒成立?若存在,求出a的最大值;若不存在,说明理由.
分析 (Ⅰ)求出函数的导数,根据函数的单调性;
(Ⅱ)求出函数的导数,得到a≤e,问题转化为证明当a=2时,不等式恒成立,设$g(x)=\frac{e^x}{x^2}-\frac{2}{x}-lnx$,根据函数的单调性证明即可.
解答 解:(Ⅰ)证明:当a=2时,f(x)=ex-x2,则f'(x)=ex-2x,
令${f_1}(x)=f'(x)={e^x}-2x$,则${f'_1}(x)={e^x}-2$,
令f'1(x)=0,得x=ln2,故f'(x)在x=ln2时取得最小值,
∵f'(ln2)=2-2ln2>0,∴f(x)在(0,+∞)上为增函数,
∴f(x)>f(0)=1;
(Ⅱ)f'(x)=ex-ax,
由f'(x)≥x2lnx,得ex-ax≥x2lnx对一切x>0恒成立,
当x=1时,可得a≤e,所以若存在,则正整数a的值只能取1,2.
下面证明当a=2时,不等式恒成立,
设$g(x)=\frac{e^x}{x^2}-\frac{2}{x}-lnx$,则$g'(x)=\frac{{({x-2}){e^x}}}{x^3}+\frac{2}{x^2}-\frac{1}{x}=\frac{{({x-2})({{e^x}-x})}}{x^3}$,
由(Ⅰ)ex>x2+1≥2x>x,∴ex-x>0(x>0),
∴当0<x<2时,g'(x)<0;当x>2时,g'(x)>0,
即g(x)在(0,2)上是减函数,在(2,+∞)上是增函数,
∴$g(x)≥g(2)=\frac{1}{4}({{e^2}-4-4ln2})>\frac{1}{4}({{{2.7}^2}-4-4ln2})>\frac{1}{4}({3-ln16})>0$,
∴当a=2时,不等式恒成立,
所以a的最大值是2.
点评 本题考查了函数的单调性问题,考查导数的应用以及函数恒成立问题,是一道中档题.

| A. | (1,$\frac{9}{4}$] | B. | [9,+∞) | C. | (1,$\frac{9}{4}$]∪[9,+∞) | D. | [$\frac{3}{2}$,$\frac{9}{4}$]∪[9,+∞) |
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{y^2}{4}-{x^2}=1$ | C. | ${y^2}-\frac{x^2}{4}=1$ | D. | $\frac{y^2}{16}-\frac{x^2}{4}=1$ |
| A. | 4π | B. | 8π | C. | 9π | D. | 36π |
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
| A. | 3x-4y+15=0 | B. | 3x+4y-33=0 | C. | 3x-4y+15=0或x=3 | D. | 3x+4y-33=0或x=3 |
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{\sqrt{17}}{3}$ | D. | $\frac{\sqrt{13}}{2}$ |
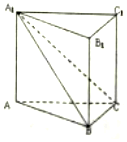 如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面ABB1A1,且AA1=AB=2.
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面ABB1A1,且AA1=AB=2.