命题:“?x∈R.x2-ax+1＜0 的否定为?x∈R.x2-ax+1≥0．题目和参考答案——青夏教育精英家教网——

题目内容

13．命题：“?x∈R，x²-ax+1＜0”的否定为?x∈R，x²-ax+1≥0．

分析直接利用特称命题的否定是全称命题写出结果即可．

解答解：因为特称命题的否定是全称命题，
所以命题：“?x∈R，x²-ax+1＜0”的否定是：?x∈R，x²-ax+1≥0；
故答案为：?x∈R，x²-ax+1≥0

点评本题考查命题的否定特称命题与全称命题的关系，基本知识的考查．

练习册系列答案

核心素养学练评系列答案

超效单元测试AB卷系列答案

单元期中期末卷系列答案

夺冠小状元课时作业本系列答案

全优大考卷系列答案

小学综合能力测评测试卷系列答案

名校学案单元评估卷系列答案

名师选优名师大考卷系列答案

孟建平各地期末试卷汇编系列答案

蓉城学堂中考总复习点击与突破系列答案

相关题目

3．已知函数f（x）=|x|+|x-4|，则不等式f（x²+2）＞f（x）的解集用区间表示为$（-∞，\;-2）∪（\sqrt{2}，\;+∞）$．

4．若集合A={x∈R|x²-3x≤0}，B={1，2}，则A∩B=（　　）

{0，1，2，3}

1．双曲线$\frac{x^2}{m}-\frac{y^2}{n}=1（{m＞0，n＞0}）$和椭圆$\frac{x^2}{a}+\frac{y^2}{b}=1（{a＞b＞0}）$有相同的焦点F₁，F₂，M为两曲线的交点，则|MF₁|•|MF₂|等于（　　）

8．△ABC的内角A，B，C的对边分别为a，b，c，若$cosC=\frac{{2\sqrt{2}}}{3}$，bcosA+acosB=2，则△ABC的外接圆的面积为（　　）

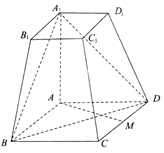如图所示，在四棱台ABCD-A₁B₁C₁D₁中，AA₁⊥底面ABCD，四边形ABCD为菱形，∠BAD=120°，AB=AA₁=2A₁B₁=2．
（Ⅰ）若M为CD中点，求证：AM⊥平面AA₁B₁B；
（Ⅱ）求直线DD₁与平面A₁BD所成角的正弦值．

5．△ABC的内角A，B，C的对边分别为a，b，c．已知$a=\sqrt{3}，b=2$，A=60°，则c=（　　）

2．在平面直角坐标系xOy中，曲线C₁的参数方程为$\left\{\begin{array}{l}x=cosα\\ y=1+sinα\end{array}\right.$（α为参数，α∈R），在以坐标原点为极点，x轴非负半轴为极轴的极坐标系中，曲线${C_2}：ρsin（θ-\frac{π}{4}）=\sqrt{2}$．
（Ⅰ）求曲线C₁的普通方程与曲线C₂的直角坐标方程；
（Ⅱ）若曲线C₁和曲线C₂相交于A，B两点，求|AB|的值．

3．矩形OABC的四个顶点坐标依次为$O（{0，0}），A（{\frac{π}{2}，0}），B（{\frac{π}{2}，1}），C（{0，1}）$，线段OA，OC及$y=cosx（{0＜x≤\frac{π}{2}}）$的图象围成的区域为Ω，若矩形OABC内任投一点M，则点M落在区域内Ω的概率为$\frac{2}{π}$．