题目内容
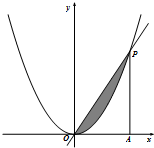 如图,直线y=kx(k>0)与函数y=x2的图象交于点O,P,过P作PA⊥x轴于A.在△OAP中任取一点,则该点落在阴影部分的概率为
如图,直线y=kx(k>0)与函数y=x2的图象交于点O,P,过P作PA⊥x轴于A.在△OAP中任取一点,则该点落在阴影部分的概率为考点:几何概型
专题:概率与统计
分析:分别求出△OAP的面积以及阴影部分的面积,利用几何概型公式解答.
解答:
解:由题意P的坐标为(k,k2),所以△OAP的面积为
×x×kx=
kx2=
k3,
阴影部分的面积为
(kx-x2)dx=(
kx2-
x3)|
=
k3,
由几何概型的概率公式得该点落在阴影部分的概率为
=
;
故答案为:
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
阴影部分的面积为
| ∫ | k 0 |
| 1 |
| 2 |
| 1 |
| 3 |
k 0 |
| 1 |
| 6 |
由几何概型的概率公式得该点落在阴影部分的概率为
| ||
|
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查了几何概型的概率公式的运用以及利用定积分求曲边梯形的面积.

练习册系列答案
相关题目
已知变量x,y,满足约束条件
,则z=3x+y的最大值为( )
|
| A、3 | ||
| B、12 | ||
C、
| ||
| D、10 |
 给出的是计算
给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |
| A、I<=100 |
| B、I>100 |
| C、I>50 |
| D、I<=50 |
不等式组
围成的区域为Ω,能够把区域Ω的周长和面积同时分为相等两部分的曲线为( )
|
| A、y=x3-3x+1 | ||
| B、y=xsin2x | ||
C、y=ln
| ||
D、y=
|
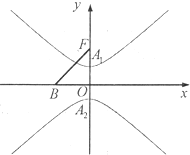 已知点A1,A2是双曲线
已知点A1,A2是双曲线| y2 |
| a2 |
| x2 |
| b2 |
A、(1,
| ||||||
B、(1,
| ||||||
C、(
| ||||||
D、(
|
对任意实数k,直线kx-y-3k+4=0与圆C:(x-3)2+(y-4)2=16的位置关系是( )
| A、相交 | B、相切 |
| C、相离 | D、与k取值有关 |
已知函数g(x)=a-x2(
≤x≤e,e为自然对数的底数)与h(x)=2lnx的图象上存在关于x轴对称的点,则实数a的取值范围是( )
| 1 |
| e |
A、[1,
| ||
| B、[1,e2-2] | ||
C、[
| ||
| D、[e2-2,+∞) |
