题目内容
设常数a≥0,函数f(x)=
.
(1)若a=4,求函数y=f(x)的反函数y=f-1(x);
(2)根据a的不同取值,讨论函数y=f(x)的奇偶性,并说明理由.
| 2x+a |
| 2x-a |
(1)若a=4,求函数y=f(x)的反函数y=f-1(x);
(2)根据a的不同取值,讨论函数y=f(x)的奇偶性,并说明理由.
考点:反函数,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)根据反函数的定义,即可求出,
(2)利用分类讨论的思想,若为偶函数求出a的值,若为奇函数,求出a的值,问题得以解决.
(2)利用分类讨论的思想,若为偶函数求出a的值,若为奇函数,求出a的值,问题得以解决.
解答:
解:(1)∵a=4,
∴f(x)=
=y
∴2x=
,
∴x=log2
,
∴调换x,y的位置可得y=f-1(x)=log2
,x∈(-∞,-1)∪(1,+∞).
(2)若f(x)为偶函数,则f(x)=f(-x)对任意x均成立,
∴
=
,整理可得a(2x-2-x)=0.
∵2x-2-x不恒为0,
∴a=0,此时f(x)=1,x∈R,满足条件;
若f(x)为奇函数,则f(x)=-f(-x)对任意x均成立,
∴
=-
,整理可得a2-1=0,
∴a=±1,
∵a≥0,
∴a=1,
此时f(x)=
,x≠0,满足条件;
综上所述,a=0时,f(x)是偶函数,a=1时,f(x)是奇函数.
∴f(x)=
| 2x+4 |
| 2x-4 |
∴2x=
| 4y+4 |
| y-1 |
∴x=log2
| 4y+4 |
| y-1 |
∴调换x,y的位置可得y=f-1(x)=log2
| 4x+4 |
| x-1 |
(2)若f(x)为偶函数,则f(x)=f(-x)对任意x均成立,
∴
| 2x+a |
| 2x-a |
| 2-x+a |
| 2-x-a |
∵2x-2-x不恒为0,
∴a=0,此时f(x)=1,x∈R,满足条件;
若f(x)为奇函数,则f(x)=-f(-x)对任意x均成立,
∴
| 2x+a |
| 2x-a |
| 2-x+a |
| 2-x-a |
∴a=±1,
∵a≥0,
∴a=1,
此时f(x)=
| 2x+1 |
| 2x-1 |
综上所述,a=0时,f(x)是偶函数,a=1时,f(x)是奇函数.
点评:本题主要考查了反函数的定义和函数的奇偶性,利用了分类讨论的思想,属于中档题.

练习册系列答案
相关题目
执行如图所示的程序框图,输出的S值为( )


| A、1 | B、3 | C、7 | D、15 |
 如图,在正方体ABCD-A1B1C1D1中,E、F、P、Q、M、N分别是棱AB、AD、DD1、BB1、A1B1、A1D1的中点,求证:
如图,在正方体ABCD-A1B1C1D1中,E、F、P、Q、M、N分别是棱AB、AD、DD1、BB1、A1B1、A1D1的中点,求证: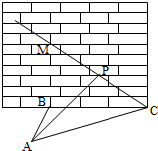 如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是