题目内容
若x0是方程(
)x=x
的解,则x0属于区间( )
| 1 |
| 2 |
| 1 |
| 3 |
A、(
| ||||
B、(
| ||||
C、(0,
| ||||
D、(
|
考点:二分法求方程的近似解
专题:计算题,函数的性质及应用
分析:由题意令f(x)=(
)x-x
,从而由函数的零点的判定定理求解.
| 1 |
| 2 |
| 1 |
| 3 |
解答:
解:令f(x)=(
)x-x
,
则f(0)=1-0>0;
f(
)=(
)
-(
)
>0;
f(
)=(
)
-(
)
<0;
故x0属于区间(
,
);
故选D.
| 1 |
| 2 |
| 1 |
| 3 |
则f(0)=1-0>0;
f(
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
故x0属于区间(
| 1 |
| 3 |
| 1 |
| 2 |
故选D.
点评:本题考查了函数的零点的判定定理的应用,属于基础题.

练习册系列答案
相关题目
对于非零实数a,b,以下四个命题都成立:
①a2+
>0;
②(a-b)2=a2-2ab+b2;
③若a2=b2,则a=±b;
④若a3-a2b>0,则a-b>0.
那么,对于非零复数a,b,仍然成立的命题的所有序号是( )
①a2+
| 1 |
| a2 |
②(a-b)2=a2-2ab+b2;
③若a2=b2,则a=±b;
④若a3-a2b>0,则a-b>0.
那么,对于非零复数a,b,仍然成立的命题的所有序号是( )
| A、①③ | B、②③ | C、①④ | D、②④ |
在复平面内,两共轭复数所对应的点( )
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、关于直线y=x对称 |
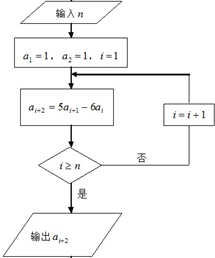 已知数列{an}满足如图所示的程序框图.
已知数列{an}满足如图所示的程序框图.